ELEC271 W5-6
本博客草草创建,简陋不堪。本人才疏学浅,笔记也不过给诸君作一参考。如有疑惑/错漏/建议 还请使用这个匿名提问箱,我会一一回复。 不过现在本博客也增加了评论功能,你也可以直接在底下说。不过这个评论功能没有提醒……回复可能会不够及时。
https://www.tapechat.net/uu/5r0pL8/ZV9H0543

WEEK5 Frequency Response
Frequency Response这玩意儿我感觉一直似乎处在 “懂的都懂,不懂的我也不好说” 的情况。总之让我看看好不好说……
对于理想的纯电阻电路,是不存在frequent response这种东西的。但是只要我们加了什么二极管三极管,其实电路里就不可避免存在一些电容或者电感。那么课上也很明显可以看到,我们一般不讨论电感只考虑电容。而这些元器件它们的阻抗和电信号的频率是有关系的,因此叫frequency response。
| 东西 | 阻抗 | 性质 |
|---|---|---|
| 电阻 | \(Z=R\) | 一视同仁 |
| 电容 | \(Z=\frac{1}{j\omega C}\) | 低频高阻,高频低阻 |
| 电感 | \(Z=j\omega L\) | 低频低阻,高频高阻 |
首先我们对三极管进行一个典中点典之电路近似:

把一个网格电路变成单纯的并联。
此时考虑be两段电压,\(\mathrm{v}_{\mathrm{b}^{\prime} \mathrm{e}}=\mathrm{i}_{\mathrm{i}}\left(\mathrm{r}_{b^{\prime}e} / / \mathrm{Z}_{c}\right)=i_{i} \frac{r_{b'e} / j \omega C}{r_{b^{\prime} e}+1 / j \omega C}\)且\(i_o=g_m\mathrm{v}_{b'e}=\beta_0i_i\) 于是: \[ A_{i} \equiv \frac{i_{o}}{i_{i}}=\frac{-g_mr_{b'e} / j \omega C}{r_{b^{\prime} e}+1 / j \omega C}=-\frac{g_mr_{b'e}}{r_{b^{\prime} e}j \omega C+1}=-\frac{\beta_0}{1+j \frac{\omega}{1/r_{b^{\prime} e}C}}=-\frac{\beta_0}{1+j \frac{\omega}{\omega_0}} \] 其中,\(\omega_0=\frac{1}{r_{b^{\prime} e}C}\)
还可以写成有关频率的形式(\(\omega=2\pi f\), \(f_0=\frac{1}{2\pi r_{b^{\prime}e}C}\)) \[ A_{i}=-\frac{\beta_0}{1+j \frac{\omega}{\omega_0}}=-\frac{\beta_0}{1+j \frac{f}{f_0}} \] 然而这是个复数,我们其实更看重放大倍数的绝对值。那么就求复数模长: \[ |A_{i}|=\frac{\beta_0}{\sqrt{1+(\frac{f}{f_0})^2}} \]
然后不同的频率会有不同的放大倍数,就得到了频率响应。
不过这丢失了复数自带的相位信息,因此还会有一个相位图: \[ \varphi=-arctan(\frac{f}{f_0}) \] 以下面这个简单的电路为例, 其中\(R=1/\pi\ \ohm,\ \ C=1/2\ mF,\ \ f_0=\frac{1}{2\pi RC}=1\ kHz\)
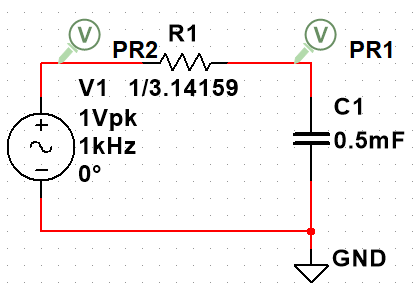 \[
A_{i}=\frac{V_{o}(1)}{V_{i}(2)}=\frac{\frac{1}{j\omega
C}}{R+\frac{1}{j\omega C}}=\frac{1}{1+j\omega
RC}=\frac{1}{1+j\frac{f}{f_0}}
\] 由此方程可以得到,我们的\(|A_{i}|\)在1k迎来拐点,而此时的相位差\(\varphi=-arctan(\frac{f}{f_0})=-arctan(1)=-45°\)
如图:
\[
A_{i}=\frac{V_{o}(1)}{V_{i}(2)}=\frac{\frac{1}{j\omega
C}}{R+\frac{1}{j\omega C}}=\frac{1}{1+j\omega
RC}=\frac{1}{1+j\frac{f}{f_0}}
\] 由此方程可以得到,我们的\(|A_{i}|\)在1k迎来拐点,而此时的相位差\(\varphi=-arctan(\frac{f}{f_0})=-arctan(1)=-45°\)
如图:

值得注意的是,我们之所以可以得到这样看上去很简单的图,是因为dB是指数增长的单位,伯德图是对数指标,于是指数增长/减小的曲线便被“扭曲”成了斜率或正或负的直线了。
既然已经和直线差不多了,我们不如更进一步:直接用折线段近似:
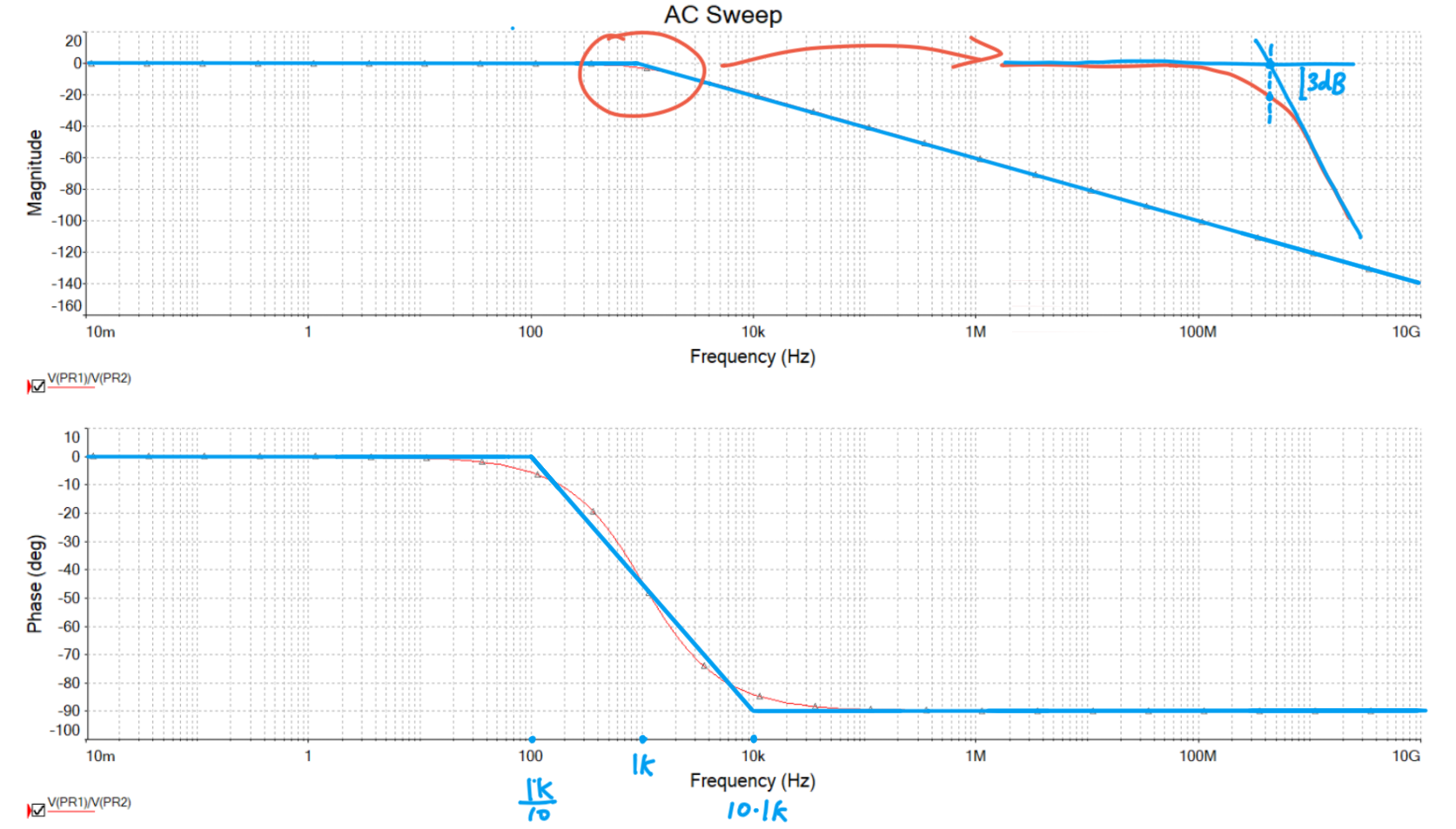
而这就和我们207学的不谋而合了。
Miller effect
回到三极管。之前那个神中神模拟其实不够完善。
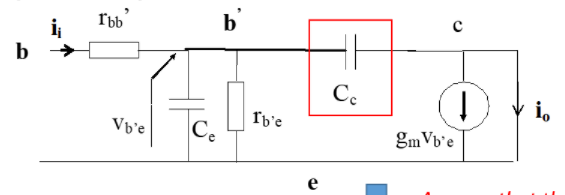
观察\(C_c\) , 它最特殊的地方在于,连接了输入输出两端,使得分析变得复杂。能不能把它等效拆解到两边去呢?有请Miller’s Theorem:
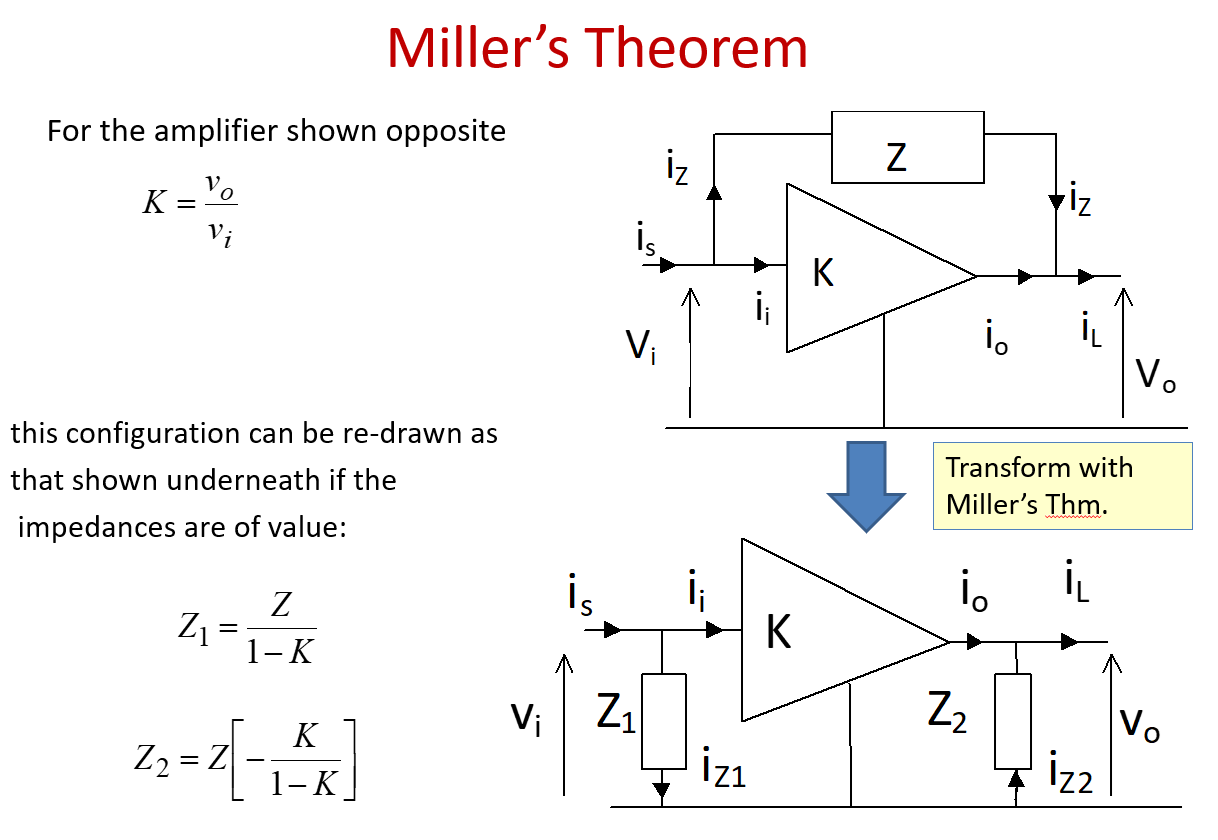
证明:
\(K=i_o/i_i\) , \(i_{Z}=i_{Z1}=i_{Z2}\) , \(Z_1=v_{i}/i_{Z1}\) , \(Z_2=-v_{o}/i_{Z2}\)
\[ i_{Z}=\frac{v_{i}-v_{o}}{Z}=\frac{v_{i}}{Z}\left(1-\frac{v_{o}}{v_{i}}\right)=\frac{v_{i}}{Z}(1-K)=\frac{v_{i}}{Z/(1-K)} \]
\[ Z_1=\frac{v_{i}}{i_{Z1}}=\frac{v_{i}}{i_{Z}}=\frac{Z}{1-K} \]
\[ Z_2=-\frac{v_{o}}{i_{Z2}}=-\frac{K v_{i}}{i_{Z}}=-\frac{K}{1-K}Z \]
由于阻抗适用于电阻/电容/电感/混合电路,因此是可以用于化简电容的。于是我们得到了相对严谨的三极管等效电路图:
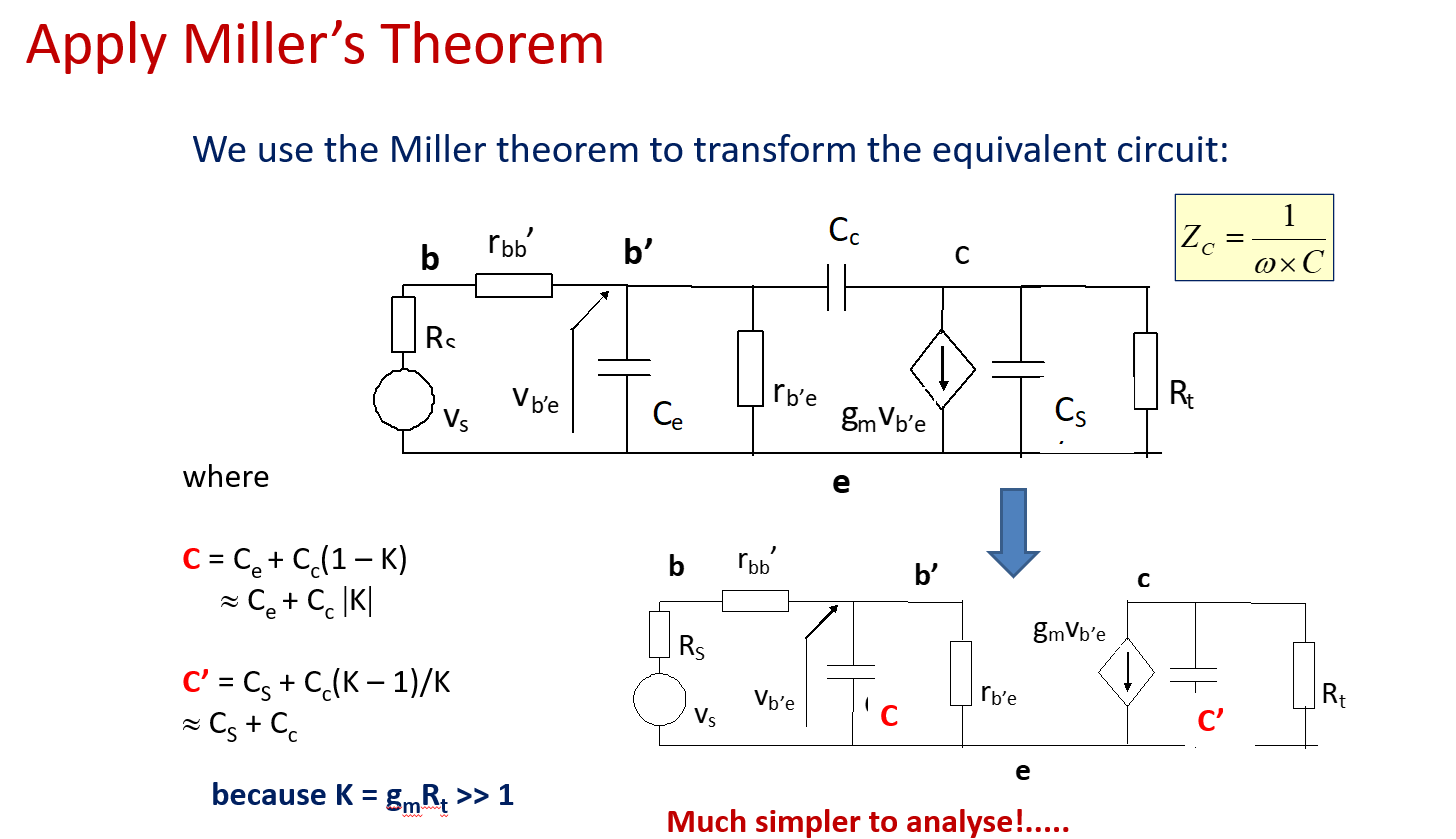
WEEK6 MOSFET based amplifiers + Step Response of Amplifiers
MOSFET
有关MOSFET的具体内容可以详见我EEE109笔记的W3-4和W5-10部分:https://luobutan.com/categories/EEE109/
本课中,该 \(\beta\) 就是我们当初学的 \(K_n\) , \(\lambda\) 是厄利电压的倒数: \(V_{A}=\frac{1}{\lambda}\)
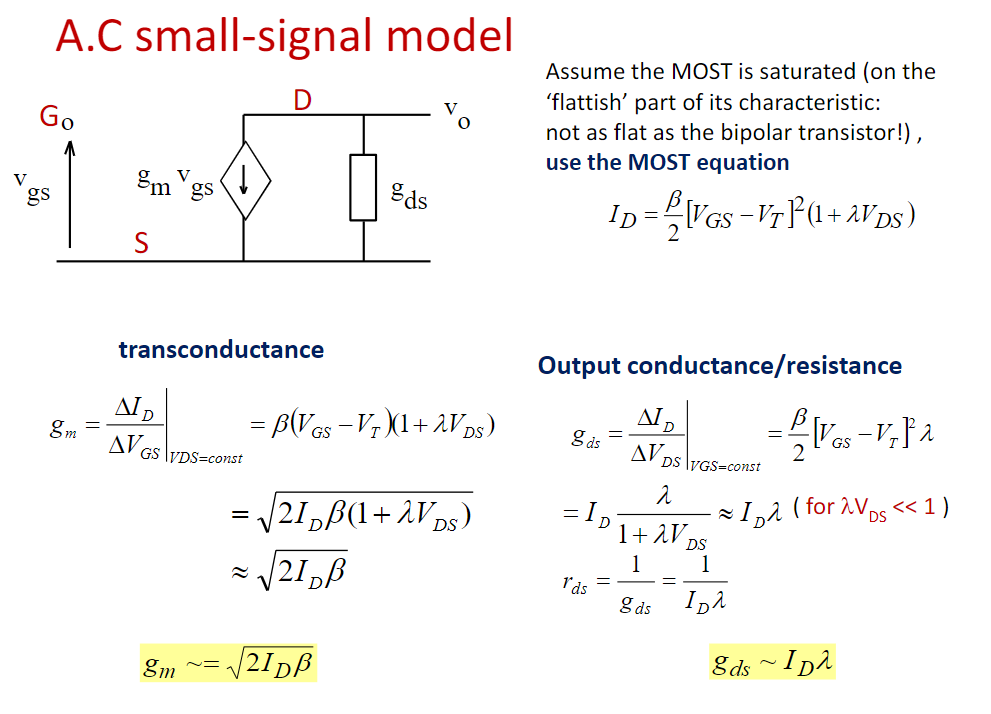

不过,三极管的电容都要考虑了,mos管自然也逃不掉:
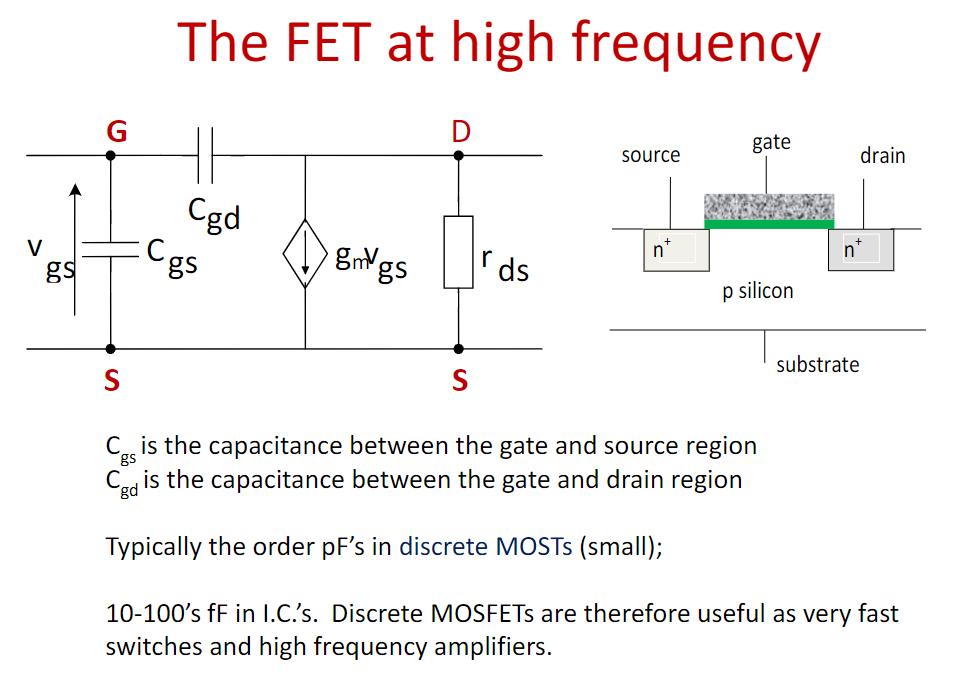
还是一样,先忽略 \(C_{gd}\) 在输出端的影响,将两个电容视作并联,算出响应转折频率:
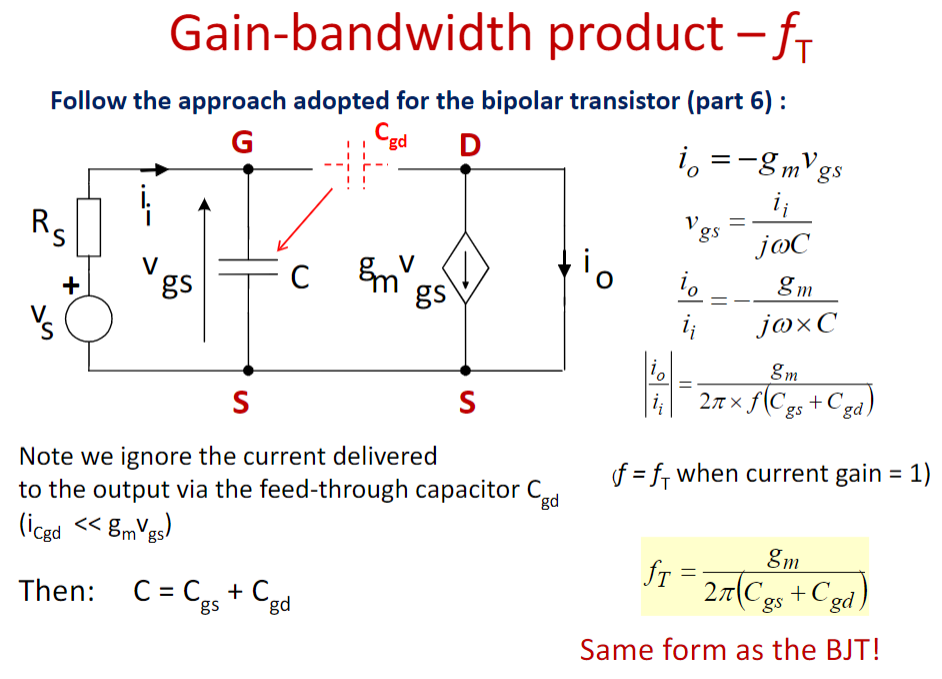
然后和三极管一样,用Miller’s Theorem 把\(C_{gd}\)等效拆解到两边去:
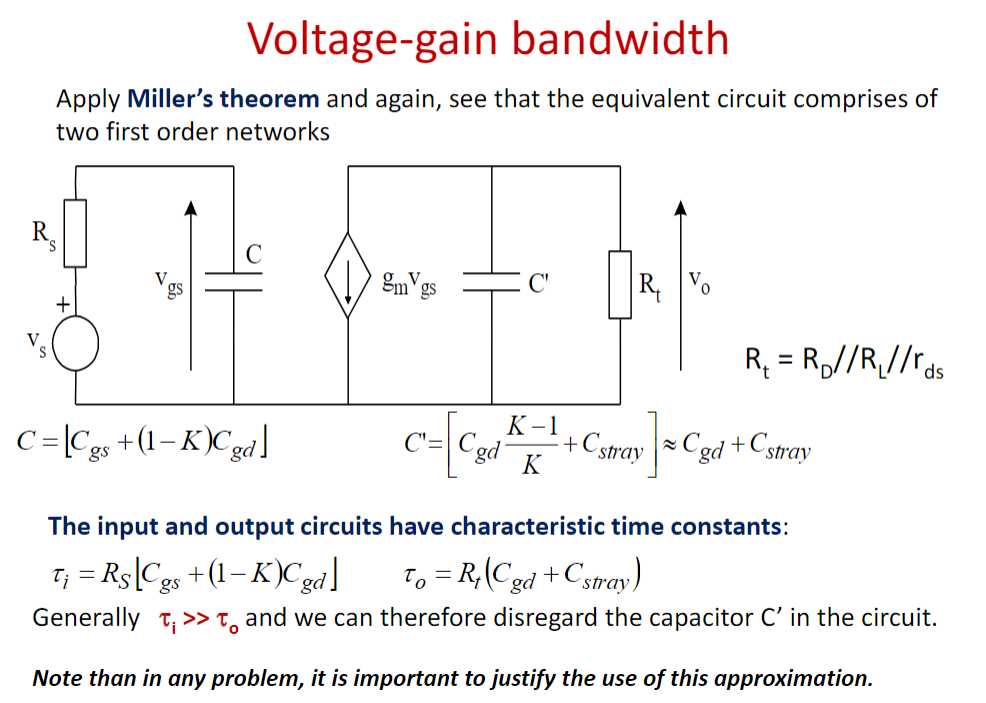

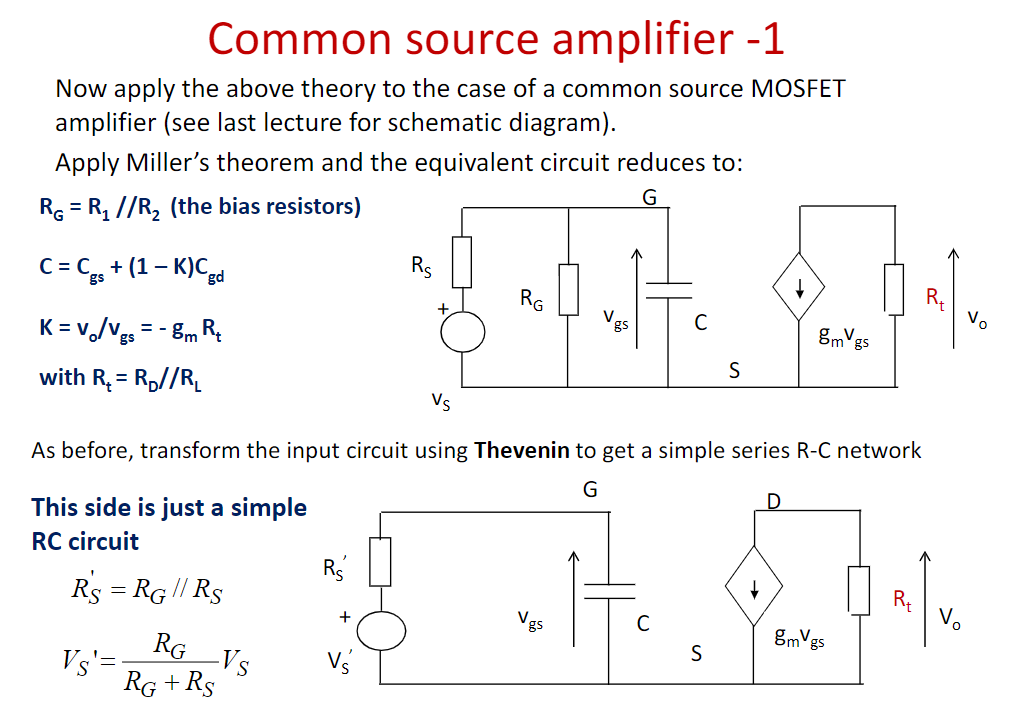
amplifiers
这里感觉可能就是举个例子。
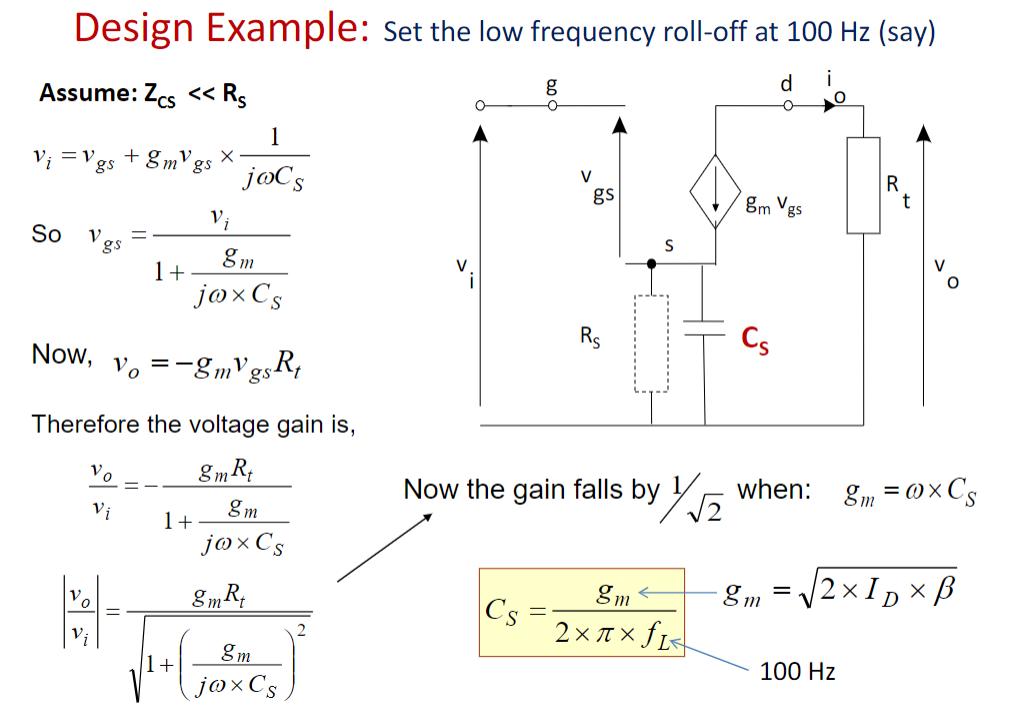
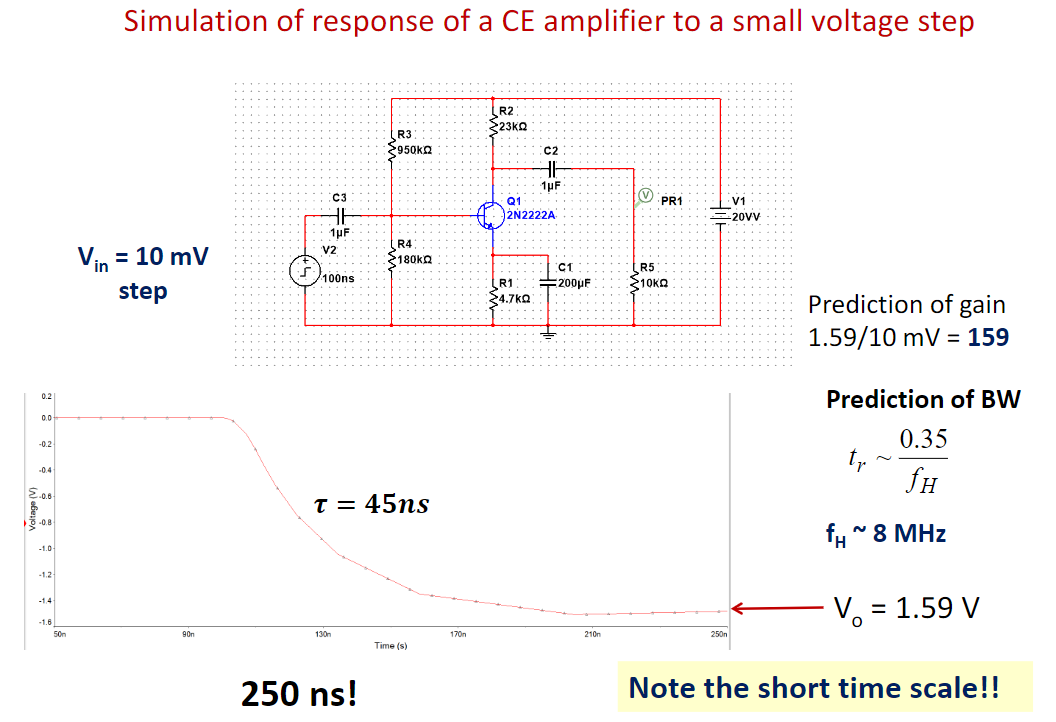
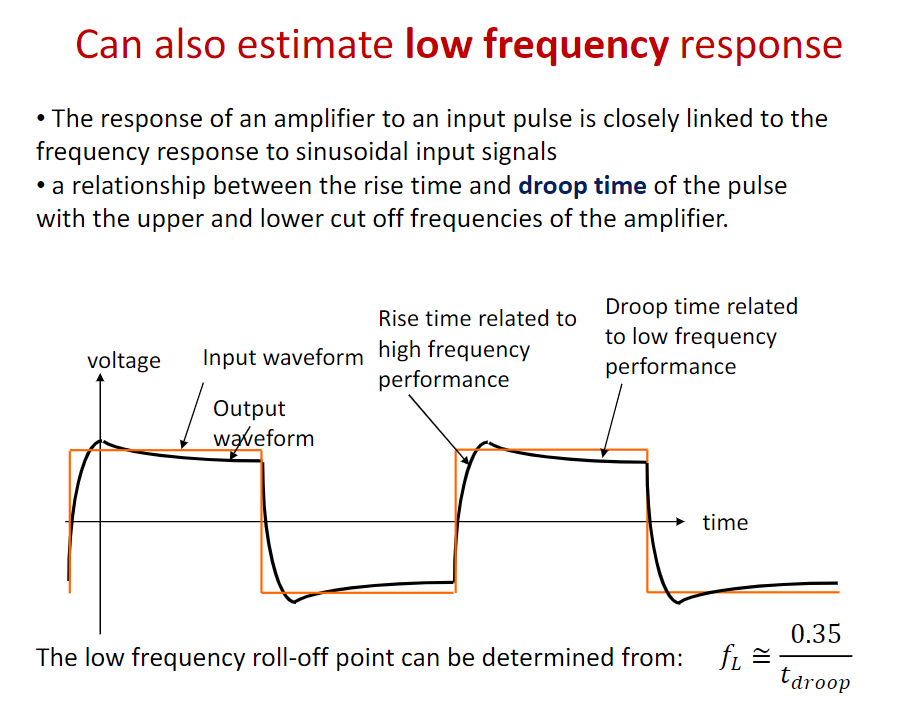
Step Response
这部分感觉没什么内容,ppt已经讲完了。如果接下来复习发现有东西再说吧
频率响应是放大器在频域的性质。而在时域的性质可以用Step Response来体现。


响应图像如此:其实和普通RC电路没什么区别