ELEC271 W3-4
本博客草草创建,简陋不堪。本人才疏学浅,笔记也不过给诸君作一参考。如有疑惑/错漏/建议 还请使用这个匿名提问箱,我会一一回复。 不过现在本博客也增加了评论功能,你也可以直接在底下说。不过这个评论功能没有提醒……回复可能会不够及时。
https://www.tapechat.net/uu/5r0pL8/ZV9H0543

WEEK3 Differential Amplifier
Differential Amplifier: 两个小输入,两个大输出。
Differential mode:输出相减,去掉直流值得到放大的小信号。
Common mode:输出相加,去掉相反的小信号得到放大的基波——比如直接放大交流信号。
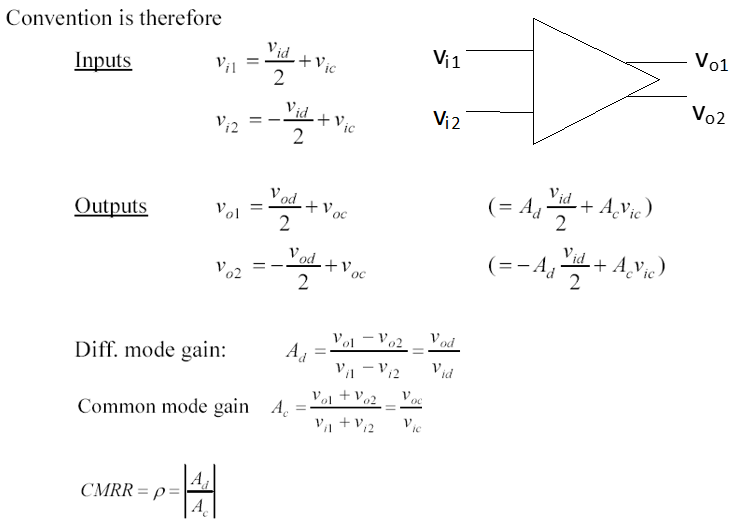
正如所有函数都可以视为应该一个偶函数和一个奇函数之和,设两个任意输入为 \(V_{\text {in }}^{+}\) 和\(V_{\text {in }}^{-}\) , 我们都可以看作Differential mode 和 Common mode 结果之和: \[ V_{\text {out }}=A_{\mathrm{d}}\left(V_{\text {in }}^{+}-V_{\text {in }}^{-}\right)+A_{\mathrm{c}} \frac{V_{\text {in }}^{+}+V_{\text {in }}^{-}}{2} \] 考虑到\(A_{\mathrm{c}}\) 常常极小,所以信号之和变化在输出端的影响可以忽略不计。于是,一端接地一端输入(单端输入)变成了计算\(A_{\mathrm{d}}\)常用的手段。这在lab5中也有所体现。
值得注意的是,虽然 单端输入 不会改变 Voltage gain,但 单端输出 会。因为单端输入依然会同时改变\(V_{\text {o1}}\)和\(V_{\text {o2}}\),\(V_{\text {out}}/V_{\text {in}}\)比值依旧。可单端输出却只取了其中一个,Voltage gain 自然需要砍半。
直流分析
默认 vi1 = vi2 = 0
\(v_{i1} = v_{ic} + v_{id}/2 = v_{id}/2\)
\(v_{i1} = v_{ic} - v_{id}/2 = v_{id}/2\)
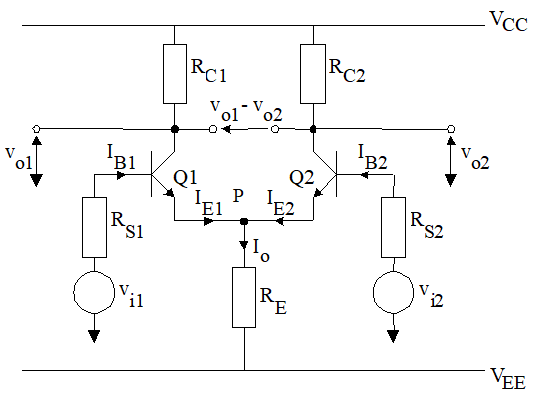
\(I_o = (v_{i1} + v_{i2} - V_{EE} - 0.7) / R_E= ( |V_{EE}|- 0.7 ) / R_{E}\)
\(V_p = R_E*I_o\) ——p点电压稳定
那么对于两个三极管的直流偏置电流:\(I_c = I_o / 2\)
可见,\(I_o\)越稳定, Differential amplifier的直流偏置就不会波动,工作状态就更稳定。所以后期我们会把\(R_{E}\)换成电流源,不过这是第4周的内容了。
交流分析
\(g_m = 40I_c = 20I_o\)
因为小信号电压越大,\(i_c\) 越大,\(R_c\)两端电压差就越大。
而在交流分析中,由于\(v_{id}=v_{i1}-v_{i2}\) , \(v_{od}=v_{o1}-v_{o2}\) , 且小信号部分等大相反, 因此以\(\pm v_{id}/2\)和\(\pm v_{od}/2\)指代。
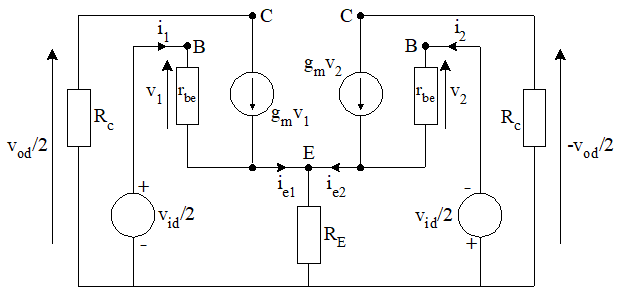
于是,\(i_{e1}=-i_{e2}\) , \(R_E\) 无电流,两端电压相等,可视作短路,为接地的一部分。
考虑到两边实际上是对称的,我们只需要分析一边即可,于是拎出来:
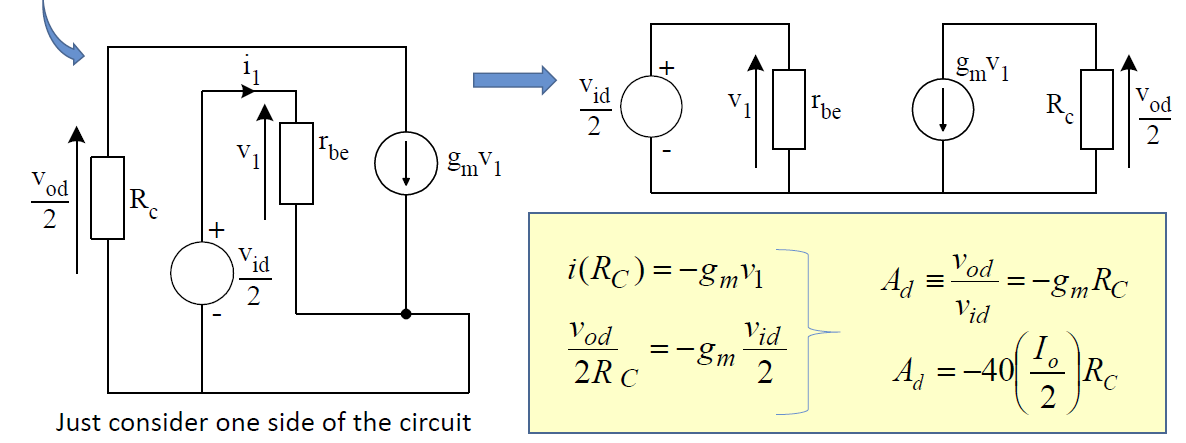
可见,此时该电路对于小信号的增益是负的:
\(A_d = v_{od}/v_{id} =-g_m R_c=-20I_{o}R_c\) ——虽然绝对值 \(|A_d|>1\)
但如果我们考虑单端输出,也就是把两端得到的电压挨个分析,虽然该电路是对称的,但由于我们定义的输入\(v_{id}=v_{i1}-v_{i2}\) 对于两端而言是相反的,因此\(A_{d1}\)和\(A_{d2}\)也会相反: \[ \left\{\begin{array}{l} A_{d 1}=\frac{v_{o 1}}{v_{i 1}-v_{i 2}}=-g_{m} \frac{R_{C 1}}{2} \\ A_{d 2}=\frac{v_{o 2}}{v_{i 1}-v_{i 2}}=+g_{m} \frac{R_{C 2}}{2} \end{array}\right. \] 输入电阻:input resistance \(R_{id}\)
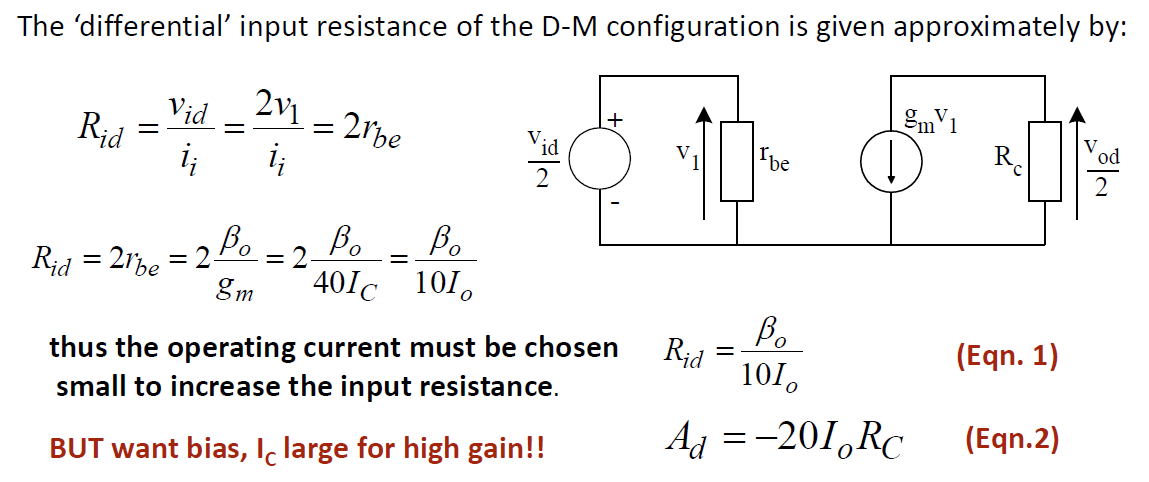
Common-mode inputs 共模输入
所谓Common-mode input 指两边的输入信号一模一样。
此时,在交流分析中 \(R_E\) 不再可以视作短路。为了方便我们拆出其中一半来分析,我们就把\(R_E\)拆成两个\(2R_E\)并联:
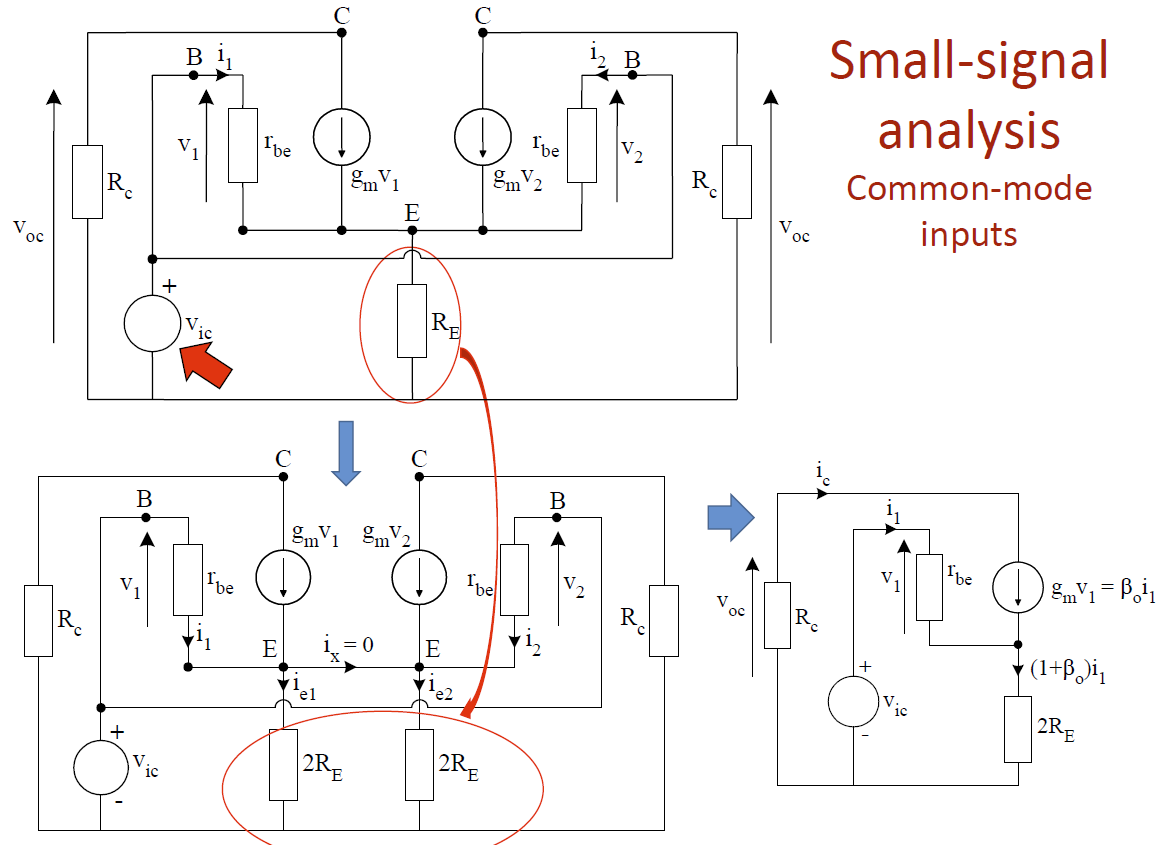
这其实就变成了两个并排的CE-ED:`
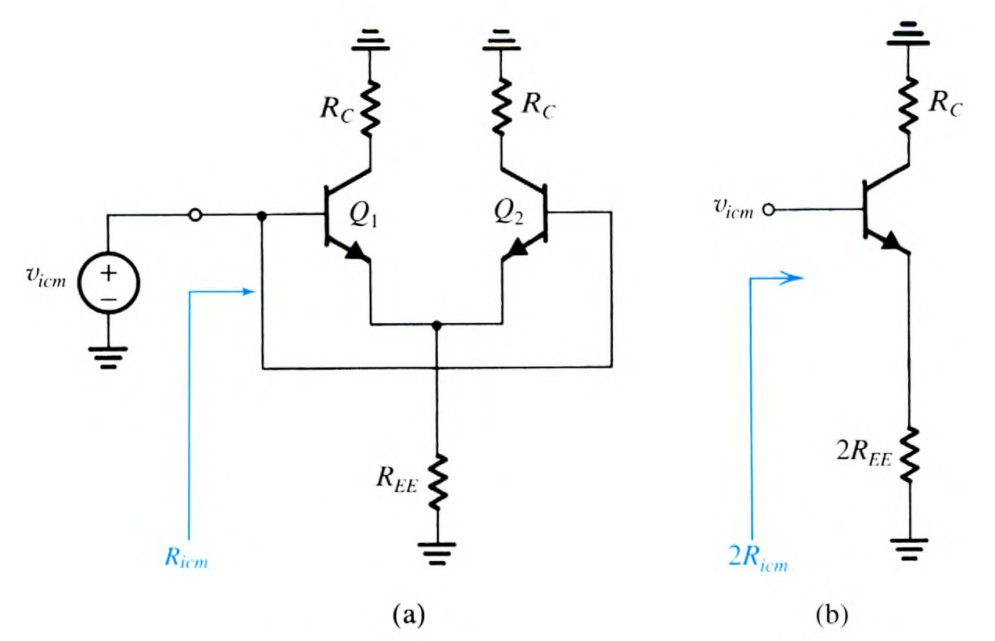
分析其中一个,套CE-ED的公式就完了。
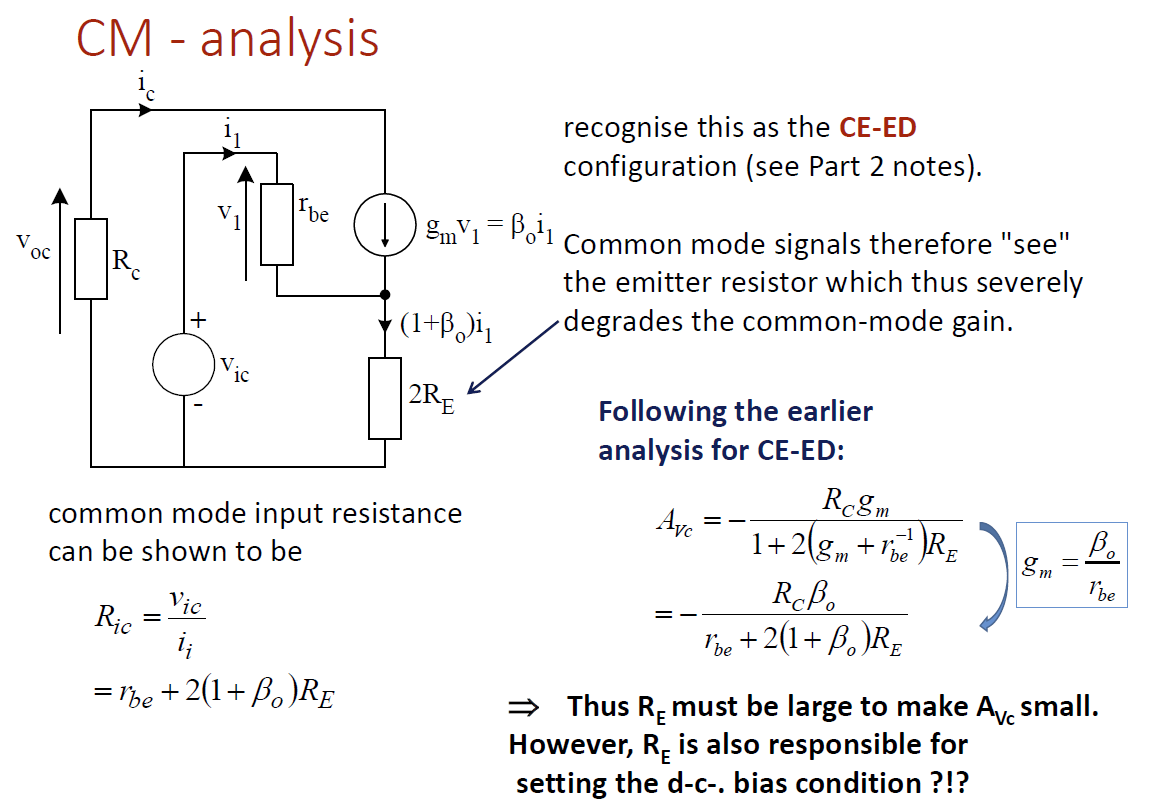
可见,\(R_E\) 越大,\(A_c\) 越小。但单纯增加\(R_E\)是没用的,那你直接断路不就得了?肯定不行。很明显,单纯的大电阻反而会破坏差分放大器原本的功能。所以——有请电流源登场。
WEEK4 Current source
电流源在我们的电路设计中很重要,它常常代表了稳定——电压源提供不了恒定的电流条件。但,电压源可以拿来就用,在电路里就是一个电源,电流源可没那么简单。
电压源是天然存在的,在大部分情况下,“先有电压,再有电流” 就是一句金玉良言。如此理解,电流源其实是一种“可以灵活改变电压以便保持电流不变”的结构。为了造出这种结构,我们在此要使用三极管b极电流控制c/e极电流的特性……
CE电路就是一个简单的电流源,B极电压控制了C极电流。基于此,以下三种设计一个比一个好:
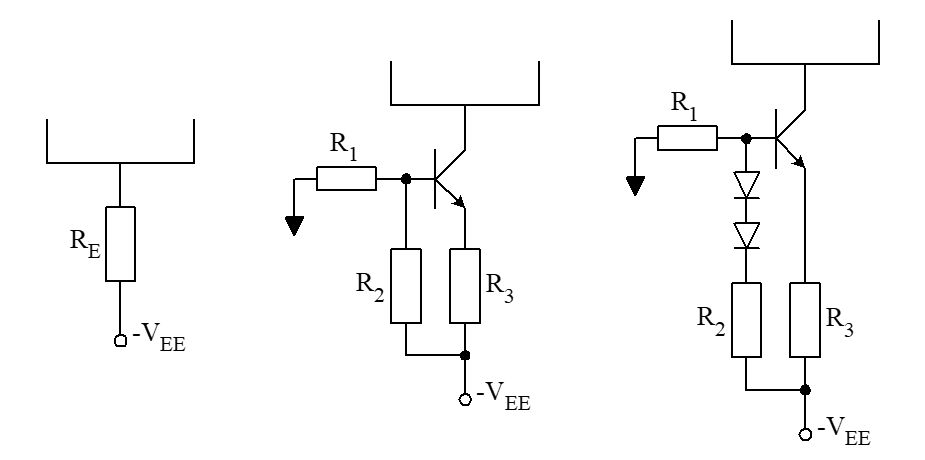
第1个就是普通的大电阻,比较菜
第2个就是普通的CE电路,比大电阻好
第3个还加上了二极管,和三极管相似的温度曲线让该设计获得了温度稳定性,在另一个维度上变得更稳定了。
- 二极管作用简析
二极管肖克莱方程:( \(V_{T}=kT/q\) ) \[ I_{D}=I_{S1} \exp \left(\frac{V_{D}}{V_{T}}\right)\\ V_{D}=V_{T} \ln \left(\frac{I_{D}}{I_{S1}}\right) \] 可见,同样的电流\(I_{D}\),温度越高,二极管两端电压\(V_{D}\)就越高,相当于二极管的电阻也越大。
三极管集电极电流: \[ I_{C}=I_{S2} \exp \left(\frac{V_{B E}}{V_{T}}\right)\left[1+\frac{V_{C E}}{V_{A}}\right] \] 由于温度越高,二极管等效电阻越高,三极管B极的电压就越高,于是\(V_{B E}\)和\(V_{T}\)同步上升,\(I_{C}\)因温度产生的变化变得更小。
我的评价是这玩意儿不会让我们就二极管的细节进行具体计算,因为: \[ I_{D}=\frac{V_{CC}-nV_{D}}{R_1+R_2}=I_{S1} \exp \left(\frac{V_{D}}{V_{T}}\right) \] 解得: \[ V_{D}=\frac{V_{CC}-nV_{T} W\left(\frac{(R_2+R_1)I_{S1}e^{V_{CC}/(nV_{T})}}{nV_{T}}\right)}{n}\\ \] 其中W代表朗伯W函数。没学过,不会。
解到这我认为这玩意确实不会让我们做计算了,至少二极管两端的电压不会是动态的模型。
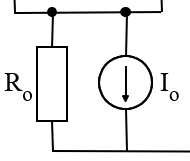
当然我们做出来的电流源从来都不是理想的电流源,比如三极管因为厄利效应,输出电流会产生一定程度的变化。这种现象基本上都可以等效成一个理想电流源并联一个电阻,我们要做的就是让这个电阻越大越好。
current mirror 电流镜
current mirror来源于一种朴素的想法:既然你的BE电压可以控制Ic,那我直接拉另一个三极管来直接给出相应BE电压不就完了?
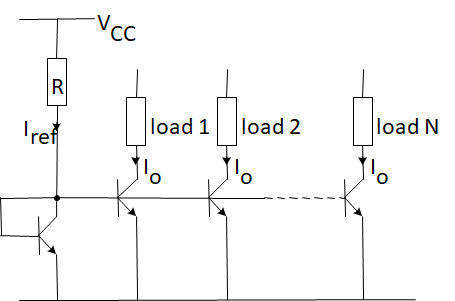
可见,在不考虑厄利效应的情况下,除了load电阻不同,这些三极管所处的状态其实是相同的——所以电流也相同。
Widlar current mirror
简单的current mirror只能重复,但Widlar要它做到自由控制——加上\(R_{E}\)
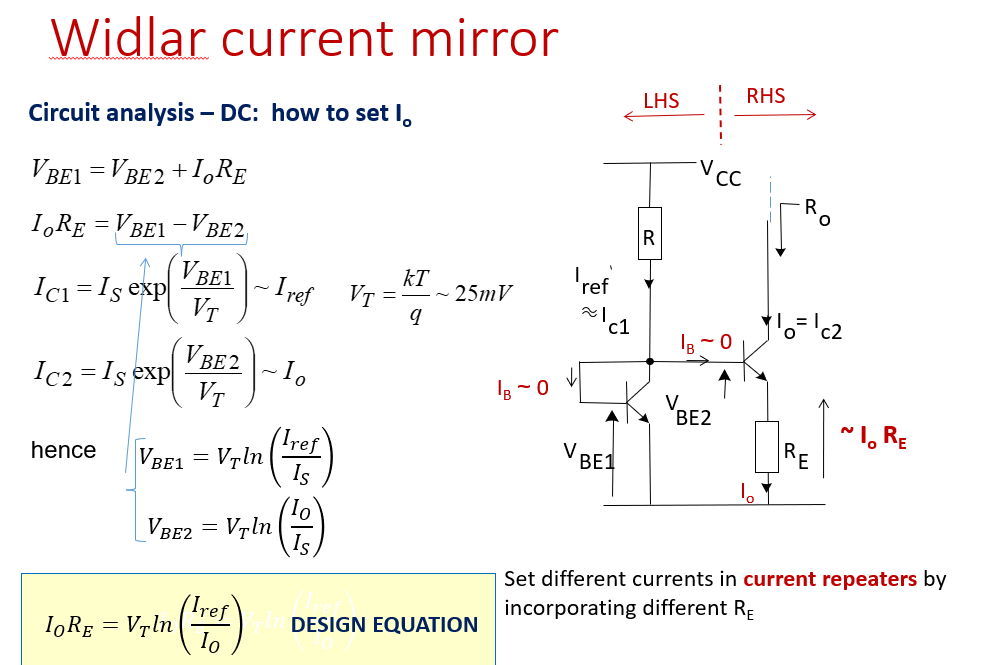
记住关键方程,我们8成就是要根据目标电流计算\(R_{E}\): \[ I_{o} R_{E}=V_{T} \ln \left(\frac{I_{r e f}}{I_{o}}\right) \] 要注意除了第1个直接接地的reference三极管外,其他三极管的\(V_{BE}\)都不一定会是0.6,反正带了电阻的肯定小于0.6,电路分析的时候不要搞错了,不然可能闹乌龙。
Active Loads 有源负载
考虑到我们目前为止学习到的东西,直流部分和小信号部分的需求常常是不同的。比如对于差分放大器,我们希望它对于小信号有高阻抗(\(R_{C}\))的同时,我们又不希望产生太大的直流压降。于是像电流镜这种电流源结构便被拿来用在了负载上:

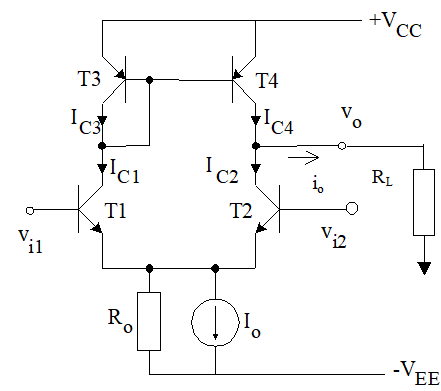
可见,为了保持电流相对稳定的同时又对小信号有较高阻抗,这样的结构如果看作单纯的电阻,其值实际上是不停变化的。因此被称作Active Loads 有源负载。
此时,这个电路结构可以看作一个差分跨导放大器:
设\(V_{i1}\)\(V_{i2}\)直流偏置都为0,输入交流信号\(V_{id}\),\(V_{i1}=V_{id}/2\), \(V_{i2}=-V_{id}/2\), \(V_{id}=V_{i1}-V_{i2}\),
考虑输出点的电流, \[ \begin{aligned} i_{o} &=I_{C 4}-I_{C 2} \\ &=I_{C 1}-I_{C 2}\\ &=g_{m} v_{i 1}-g_{m} v_{i 2}=g_{m}\left(v_{i 1}-v_{i 2}\right)\\ &=g_{m} v_{i d} \end{aligned} \]
对于交流输入,输出点的电压为:\(V_{o}=i_{o}(R_{L}//r_{ce2}//r_{ce4})=g_{m} v_{i d}(R_{L}//r_{ce2}//r_{ce4})\)
于是Voltage gain \(A_{Vd}=V_{o}/V_{id}=g_{m}(R_{L}//r_{ce2}//r_{ce4})\)
如果\(R_{L}\)非常大或者索性断路,则退化为:\(A_{Vd}=g_{m}(r_{ce2}//r_{ce4})\)
这样一番操作下来,大增益和大输入电阻都有了,CMRR也大大增加,而且输出也只需要从一边输出,而不需要求二边的差,可谓大大增强。