ELEC270 W10-11
ELEC270 WEEK10-11
前言
圣诞节:爽玩文明6。
圣诞节后:完蛋了。
如有疑惑/错漏/建议 还请使用这个匿名提问箱,我会一一回复。
https://www.tapechat.net/uu/5r0pL8/ZV9H0543

快写完了发现其实我探索的很多东西在奥本海姆那个版本信号与系统里都有过系统的讲解,感觉自己像个傻逼。如果奥本海姆那边学到什么新东西,也会加到前面的笔记里。
X.0 z Transform z变换
z变换是一个清晰简单的式子: \[ \mathcal{Z}\{x[n]\}=X(z)=\sum^{\infty}_{n=0}x[n]z^{-n} \]
以及逆z变换: \[ \mathcal{Z}^{-1}[X(z)]=x[n]=\frac{1}{2\pi i}\oint_{C}X(z)z^{n-1}dz \] 不过,如果把这变化看作是拉普拉斯变换的一个延伸,那还蛮恶心的。因为\(z=e^{sT}\)(为什么是 T 不是 t ? 因为z变换的原函数是离散的。)
X.1 重要性质
快速参考:z变换对表格与性质汇总
唯一指定重要性质: Time Delay \[ \mathcal{Z}\{x[n-a]\}=z^{-a}X(z) \] 为什么该性质重要?因为离散函数可以拆成一堆 time delay 了的 \(\delta[n]\) , 结合 \(\mathcal{Z}\{\delta[n]\}=1\) , 你哪怕不知道其他所有的z变换都可以嗯凑!甚至可以拿它当验算,算起来简单方便还错不了……
X.2 熟悉的陌生人
如果你看了我上一周的笔记关于拉普拉斯变换和幂级数视角转换的讨论,相信这一部分你肯定一点就通——或者不用点你自己就发现了。而且这是一件很有趣的事,因为当明白了我要说的这一点,你会发现他就是一句废话,他*就是*这个东西。但如果没看破没说破,可能贴在你脸上你自己都没发现。
先说结论:\(x[n]\) 就是 \(X(z)\) 洛朗展开得到的洛朗级数的负幂部分的系数序列。(因为泰勒不包含负幂,所以接下来无特殊情况该负幂部分直接用洛朗级数指代。)
例:\(z/(z-1)^2\) 展开得 \(z/(z-1)^2=\sum^\infty_{n=0}nz^{-n}\) ,而 \(n\cdot u[n]\) 对应的 \(X(z)=z/(z-1)^2\)
相当于\(\sum^\infty_{-\infty}z^{-n}\) 的系数序列乘上了\(n\cdot u[n]\)
于是所谓Z变换就变成了复变函数洛朗展开的传统数学问题。
然后用这个视角看逆z变换就变得非常简单好理解了:围道积分只能求出洛朗级数\(z^{-1}\)时的值,因此给函数乘上 \(z^{n-1}\) 求出每一级得到洛朗级数序列——通用的展开方法罢了。
值得注意的是,我们的变化是有意义的:
\(x[n]\) 的信号是有时间顺序的。
\(\xleftarrow{\ \ \ \ \ \ \ \ \ \ \ past\ \ \ \ \ \ \ \ \ \ }now\xrightarrow{\ \ \ \ \ \ \ \ \ \ future\ \ \ \ \ \ \ \ \ \ }\)
\(\cdots \ \ z^{3}\ \ z^{2}\ \ z^{1}\ \ z^{0}\ \ z^{-1}\ \ z^{-2}\ \ z^{-3}\ \ \cdots\)
\(\xleftarrow{\ \ \ \ \ \ \ \ \ \ \ 泰勒\ \ \ \ \ \ \ \ \ \ }展开\xrightarrow{\ \ \ \ \ \ \ \ \ \ \ 洛朗\ \ \ \ \ \ \ \ \ \ \ \ \ }\)
考虑到课上我们接触到所有的z变换都是causal的,这就意味着我们只会遇到跟洛朗级数相关的情况。当然,这不代表z变换就不存在使用泰勒展开的情况,毕竟严格来说,泰勒展开是洛朗展开的一个子集。但(正幂)泰勒展开就意味着非causal的 \(x[n]\) ,ROC也会有所不同。 参见 X.3
X.2.5 笔记背后的故事
您若对此没有兴趣,可以通过博客侧边目录跳转到 X.3
当时我在做Z变换problem sheet的时候,对于其中一道题用了两个方法作答,发现他们出现了矛盾。不过我课上询问老师时老师表示他也不知道。让我po在discussion board 上以便后续解答。
我在discussion board 上的提问↓ 你也可以先别急着往下拉,跟着想想。如果没有被我绕进沟里,那说明你已经明白X.2的内容。

OK. But first, I need to clarify to you… this question is a little bit tricky. It's a special case in this situation.
好吧,上面那句英文是防止你余光一不小心瞄到答案。我想说,这仅仅是针对这个函数的特例。
因为\(u[n]\)的取值并不随着时间的推演而变化,它可以直接相减。这就是为什么两个方法都能用的原因,然而事实上只有洛朗才是通用的。对于其他函数,泰勒级数和洛朗级数得到的结果将会不同。
插曲
你所见到的思路是我整理过后的。事实上,我是先遇到这个问题,再学会拉普拉斯变换和幂级数视角转换的。那真是一段恶心的寻找之旅,因为你懂的……z变换就是洛朗展开本身,答案就在我眼皮子底下。我不可能找到其他任何更高级的,有关于z变换某种应用/性质/联系的解释,因为它就是它自己。
有趣的是,我是在睡梦中得到的答案。

X.3 ROC region of convergence 收敛域
1. region of convergence,显然不会包含奇点在内。所有ROC不含奇点 2. 幂级数的收敛与否只和|z|相关,所以收敛域是一个圆盘/圆环
若\(x[n]\)只有有限个,它就只是一堆幂函数的和,而不是幂函数逼近某个函数的极限,除了0和无穷远处,这个和都是有限的。
引出性质:
3. 若 \(x[n]\) 为有限长序列,ROC为整个复平面(可能去除z=0/无穷远点)
现在,设 \(X(z)\) , 有多个奇点。
对于我们causal的 \(x[n]\) ,也就是纯负幂洛朗级数,它将不含任何正幂的泰勒部分,因此必然包含无穷远点。
它的ROC应该是这个样。
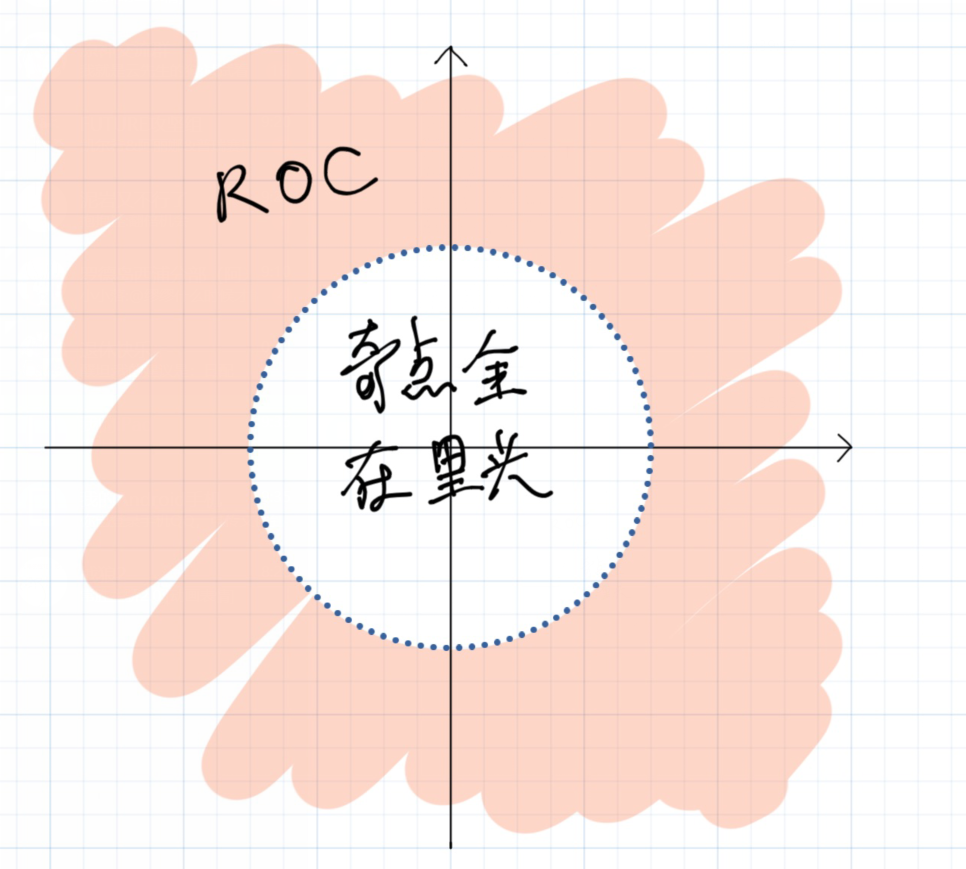
引出性质:
4. 对于causal的 \(x[n]\),设最外围的极点\(|z_0|=r_0\),则所有\(|z|>r_0\)都在ROC内
反之,
5. 对于只有n<=0项的 \(x[n]\)(左边序列),设最内部的极点\(|z_0|=r_0\),则所有\(|z|<r_0\)都在ROC内(极点全在外头的实心圆盘)
再混合,
6. 对于两边都有的,把它拆成上述两种序列,ROC取交集。
这种情况分为两种可能
- 交集是圆环,那么ROC就是一个圆环。
- 交集为空,则无ROC,\(X(z)\) 不存在。
值得注意的是,当\(|z|=1\), \(z=e^{i\omega}\), z变换退化成傅里叶变换, 因此可以根据ROC是否包含单位圆来判断\(x[n]\)的傅里叶变换是否收敛。
而考虑到对于任意复数\(z=r\cdot e^{i\omega}\)
\(X(z)=X(r\cdot e^{i\omega})=\mathcal{F}\{x[n]\cdot r^{-n}\}\)
这个也有用处,不过反正咱们用不着……但有时候用这个视角去看一些问题可能会带来新的思路。