ELEC270 W8
ELEC270 WEEK8
前言
DDL越来越多,差不多把我鲨了
如有疑惑/错漏/建议 还请使用这个匿名提问箱,我会一一回复。
https://www.tapechat.net/uu/5r0pL8/ZV9H0543

Impulse Response学的东西很少,很简单,但咱们要理解为什么是Impulse Response.
8.0 Impulse Response 冲激响应
Impulse Response, 指对着一个 linear time-invariant (LTI) system (以下简称 LTI system)输入一个\(\delta(t)\),系统会输出一个\(h(t)\).
于是,对于任意输入\(x(t)\), LTI system的输出为: \(y(t)=x(t)*h(t)\)
8.1 疑惑:为什么
这东西本身没有什么问题,但是如果你之前没有接触过这个东西,你会不会产生疑问?
为什么要输入\(\delta(t)\)?其他的不行吗?Impulse Response有什么特殊的地方?
为什么其他\(x(t)\)会和\(\delta(t)\)扯上关系?凭什么\(y(t)=x(t)*h(t)\)?
为什么是\(y(t)=x(t)*h(t)\)?不能是\(y(t)=x(t)+h(t)\)?\(y(t)=x(t)h(t)\)?
8.2 解答:还是我,傅里叶!
linear time-invariant (LTI) system是傅里叶变换的天下,以上问题的解答也需要频域的视角才能作答。
首先,设想一下,对于一个Memoryless的系统,我们一直输入信号“x(t)=1”得到一个输出g(t),那么,对于任意输入x(t),可得到输出y(t)=x(t)g(t). 这样的结论想必非常好理解。
但很可惜,这里的系统只是LTI system,不一定Memoryless,怎么办呢?
好办,我们只需要把同样的过程挪到频域里操作就好辣!memory和Invertible都是相较于t而言的,通过傅里叶变换转换到频域之后,我们只需要关注线性就好了。
因为\(F(\delta(t))=1\) ,在频域,\(\delta(t)\)就是对应上文的一直输入信号“x(t)=1”,只不过变成了一直输入信号“X(\(\omega\))=1” 得到一个输出H(\(\omega\)), 逆变换到时域就是h(t).
于是,对于任意输入x(t),可得到输出\(y(t)=F^{-1}[X(\omega)H(\omega)]=x(t)*h(t)\).
因为\(\delta(t)\)在频率上包含了所有频率的分量,因此它的冲击响应刻画了整个系统的性质。(而且操作起来方便快捷。
这也就是为什么要输入\(\delta(t)\),为什么\(y(t)=x(t)*h(t)\).
当然,更主流的解释是因为任何信号的与\(\delta(t)\)卷积是它本身,于是信号可以分解成一系列\(\delta(t)\)的叠加。但我认为这个解释不够优雅(?)好吧,只是当时没想到而已。
不过我这个理解应该没什么问题,当时课上跟老师说了后他说可以。你们要是觉得这有哪里不行欢迎提问。
8.3 三兄弟响应
看图就完了
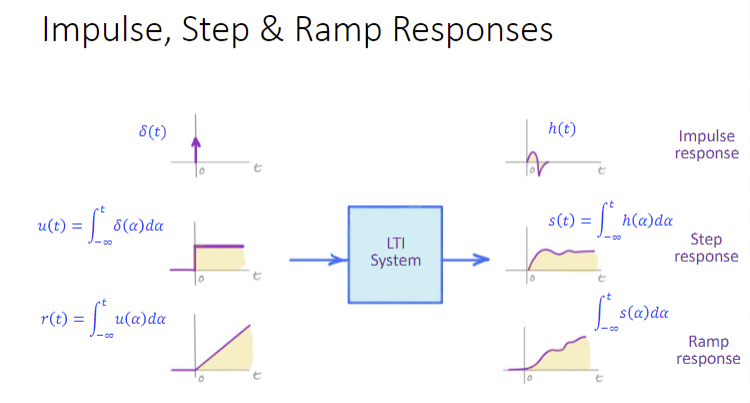
8.4 Cascaded LTI systems 级联LTI
总之就是如果一系列 LTI systems 串在一起,他们之间的顺序并不会对结果产生影响。