ELEC270 W7

发表于 2021-11-30 分类于 ELEC270 阅读次数： Valine：

跳出单纯的傅里叶——黑箱我们要多少有多少

ELEC270 WEEK7

DDL越来越多，仿佛是想把我鲨了

如有疑惑/错漏/建议还请使用这个匿名提问箱，我会一一回复。

https://www.tapechat.net/uu/5r0pL8/ZV9H0543

在老师PPT开头的章节分类里也可以看到，从这周开始我们步入了一个新的阶段。当然，是承接的，以之前的傅里叶为基础。

撇开傅里叶变换本身在数学上的意味，所谓变换既一种操作，有输入，有输出。在此，我们将其封装成黑箱，称为“system”。而对于这种高度抽象化的概念实体，若要探究总结其性质，不应尝试厘清其原理，而是观察输入输出，以及系统与系统之间的关系。

就像现实生活中做试验一样，暂不知道它们是个啥，又不能剖开研究，那如何分类？——看它们在各种操作下表现出的性质。

我们关心的性质及其试验（测试）：

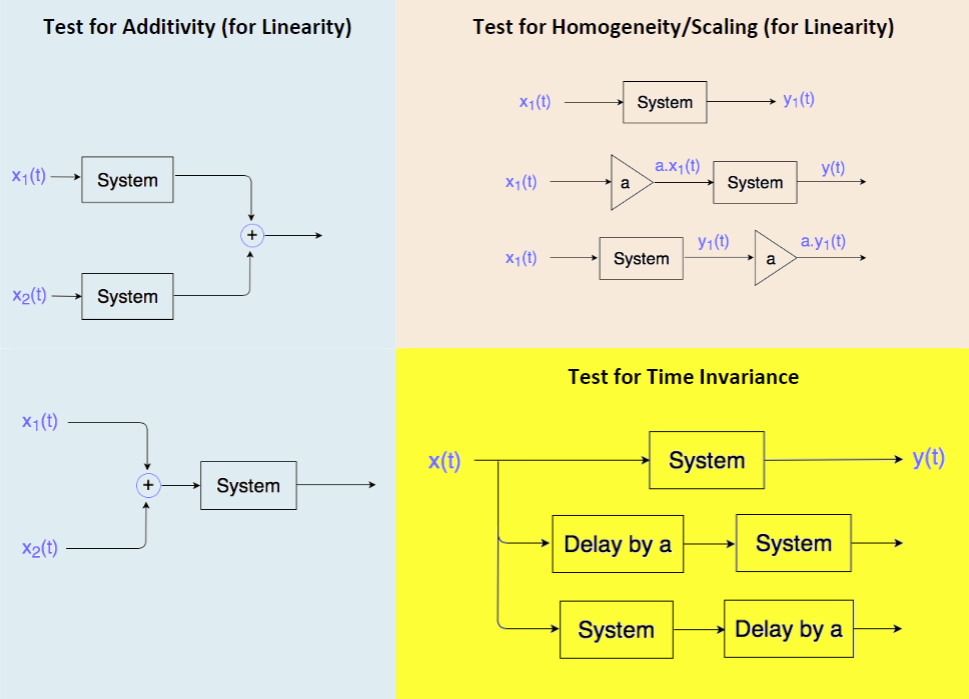
这三个性质的测试都是测试相加/数乘/延时和系统处理操作的先后顺序是否会对结果有影响。

Linearity

其中，若一个system同时满足additivity(相加)和Homogeneity(数乘)(齐次且可加)，则称其是Linearity(线性)的。

对于系统的输入x(t)和输出y(t),他们的结果有时候会产生一个时间差: x(t-a)-->y(t)。对于一个有因果关系的系统来说，必须先有输入，才有输出。

因此，当t-a<t, a>0, 则输入的时间段在输出的时间之前，因此输入是因, 输出是果，这个系统就是Causality的。

对于t-a>t, a<0, 如x(t+1)-->y(t), 这意味着在t+1时刻的输入产生了t时刻的输出——这不是现实生活中能发生的，因果性被破坏了。

如果按照官方的说法来形容，时不变性就是一个系统的输出不会因为时间的变化而改变。

这里用更容易理解的话来讲：

y(t)的表达式应是x(t)的函数，不能直接包含t的函数。t只能经过x(t)对y(t)产生影响。

Time-Varying：反义词

Memoryless Systems 静态系统：

y(t)仅与当前的x(t)有关。这样的系统仅根据输入值来改变输出，不论输入函数是什么形状，只要某时输入值相同，输出值就相同。

Memory Systems 动态系统：

y(t)和非当前的x(t-a)相关。这样的系统不仅仅根据输入值获得输出，改变输入函数的部分形状，同样会造成输出结果大不相同。比如积分。

Invertible： 对于每一个时刻t的x(t)都有独一无二的输出y(t), 这样, 我们就可以通过y(t)反推出x(t)和t了。这样的系统是Invertible，可逆的。

Non-invertible： 不可逆。顾名思义，存在同样的y(t)值对应多个t，我们没有办法通过输出完全还原输入了。

如果回顾我们之前学的傅里叶变换研究的所应用的场景，不难发现，傅里叶变换针对的是linear time-invariant system，线性时不变系统。

linear，傅里叶也是linear的。

time-invariant，无论什么时候操作，傅里叶变换都会得到相同的结果。

而这，是下一周的前提。