ELEC270 W3-6 傅里叶和他的时频分析
ELEC270 WEEK3-6 傅里叶和他的时频分析
前言
本博客草草创建,简陋不堪。本人才疏学浅,笔记也不过给诸君作一参考。如有疑惑/错漏/建议 还请使用这个匿名提问箱,我会一一回复。
https://www.tapechat.net/uu/5r0pL8/ZV9H0543

某种意义上来说,从傅里叶开始,我们才算是步入正题。
但,好消息又是坏消息,我们老师在canvas上的材料非常充分。从知识点总结到每周题目,以及题目的视频讲解,可以说是一条龙全包了。所以,如果直接按照每周讲什么讲什么的讲,我想,我这条笔记可能也没有存在的必要了。
所以在这种老师准备充分的情况下,我也就不用再注意与他每周的每周节奏严格一致了。这里我就直接把3~6周所有学的东西以主题笔记的形式进行一些总结与拓展(更多关注于“为什么”)。虽然听上去形式变自由了,但实际上写起来很难受。因为拓展太多没有意义,但不写拓展感觉又没什么好写的……真叫人便秘
不过博客好改,可以慢慢来。后续还会更新补充或查漏补缺,更新记录会在这边提到:
2021.11.8 上传
为了防止出现考试看不懂英文单词的悲剧,重要名词中能用英文的我就用英文写了。
授人以渔
3Blue1Brown 的傅里叶相关视频:链接 比我讲的好1145141919810倍,强烈建议关注
Fourier Transform 维基百科 链接
key课本 Continuous and discrete time signals and systems
一些复变函数书籍
Fourier analysis: an introduction ( Elias M. Stein, Rami Shakarchi ) 由于这本书图书馆里只有一本但被我借走了所以想看的话我准备了PDF文件
3.0 快速查找(课内笔记)
这里是week 3-6 PPT / Problem sheet 中出现过的一些非概念性知识点或问题汇总,约等于照搬ppt的注水笔记部分。也含有部分额外解释。
请善用本博客的目录系统。
week 3

\(\omega_0 =2\pi/T , \omega=2\pi f\)
因为cos负责偶函数分量 Even components,sin负责奇函数分量 Odd components
- 所以奇函数没有\(a_n\),偶函数没有\(b_n\)
由于同频率的cos函数跟sin函数实际上可以合2为1,Fourier Series 可以浓缩为Compact form:
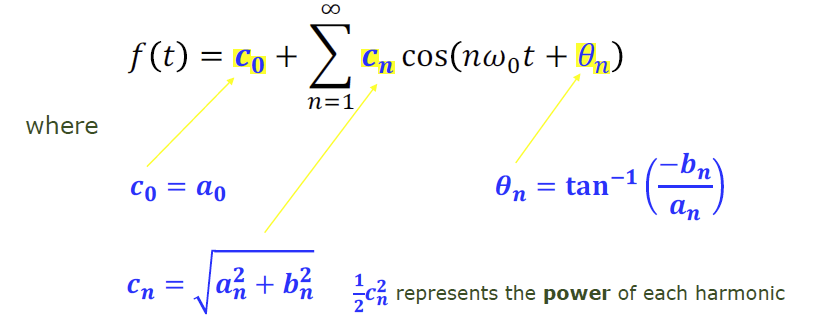
- \(c_0=a_0\) , 是直流分量 dc term
- 通过计算周期信号最大周期的积分值得到。
- 正弦波的功率是波峰平方的1/2倍
- 因为\(\int sin^2x= \int cos^2x\) , \(sin^2x+cos^2x=1\)
- Fourier Series 中除了直流分量外的每一项的频率都是基频的整数倍
对信号的操作:
| 操作 | 效果 |
|---|---|
| clipping 裁剪/削波 | 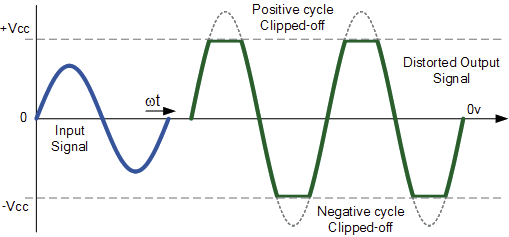 |
| clamping 钳位(电路) | 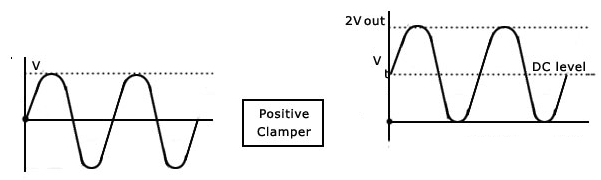 |
| Scaling 缩放 | \(f(t) \longrightarrow f(at)\) |
| Shifting 位移 | \(f(t)\longrightarrow f(t+a)\) |
week 4
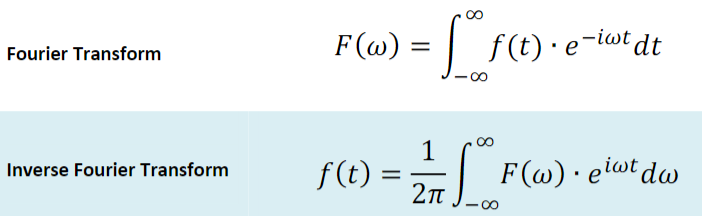
- 欧拉公式 Euler’s formula:\(e^{-i \omega t}=cos(\omega t) - i~sin(\omega t)\)
符号写法:
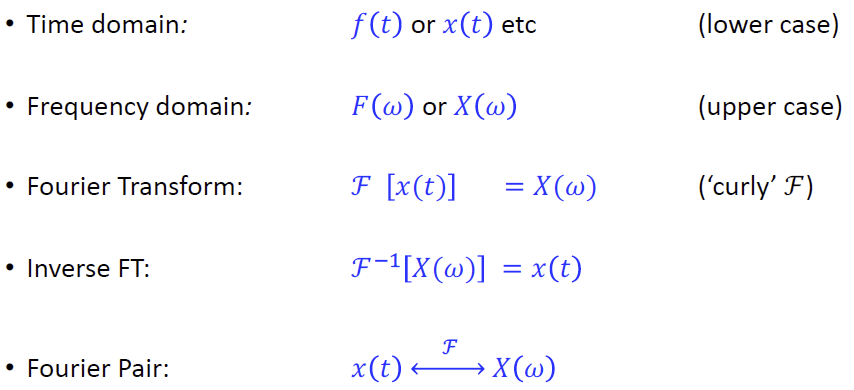
关于 sinc :
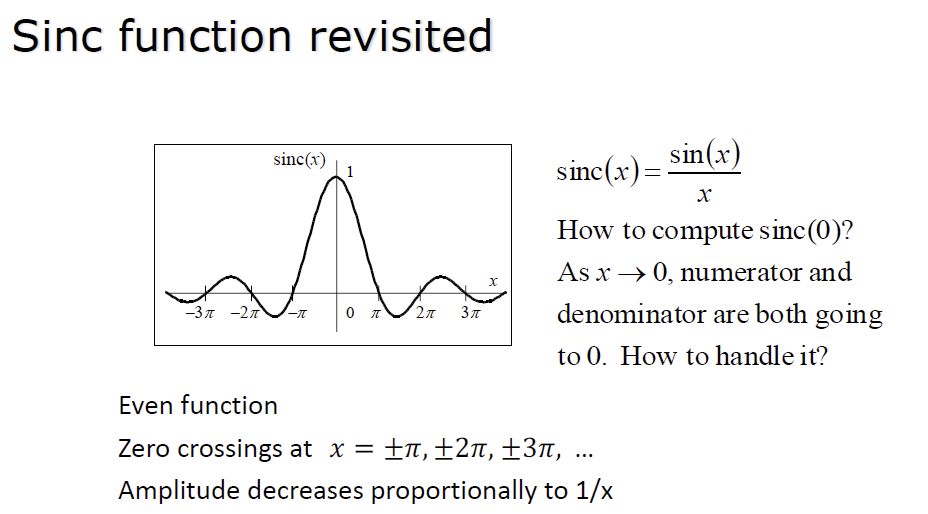

如果有你们有人去借了上图中 Reading list里面key texts的第1本,那你可能会感到困惑。因为此书中 sinc 函数的定义与ppt中不同。老师说这个函数不同的版本和教学确实有不一样的定义,以PPT上的为准。
所以请记得唯一指定 sinc :
\[
sinc(x)=\frac{sin(x)}x
\] (基本)滤波器 filter :
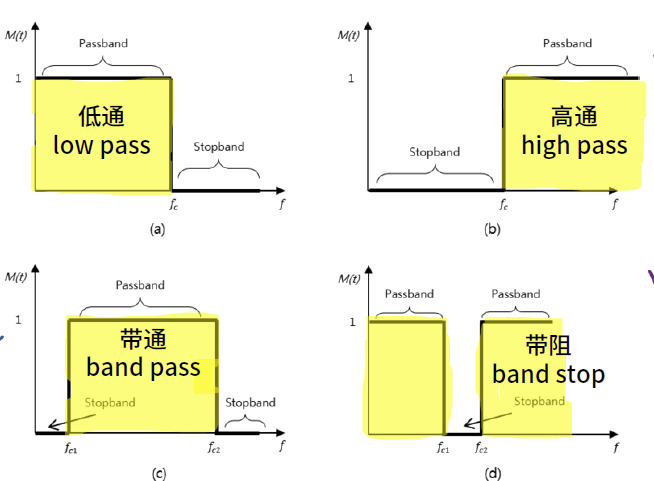
注意这只是0~f,只是右半部分!如果包含负数的频率,那么就要把上图以y轴为轴轴对称镜像一下,不能光记形状!!
Fourier Pairs :
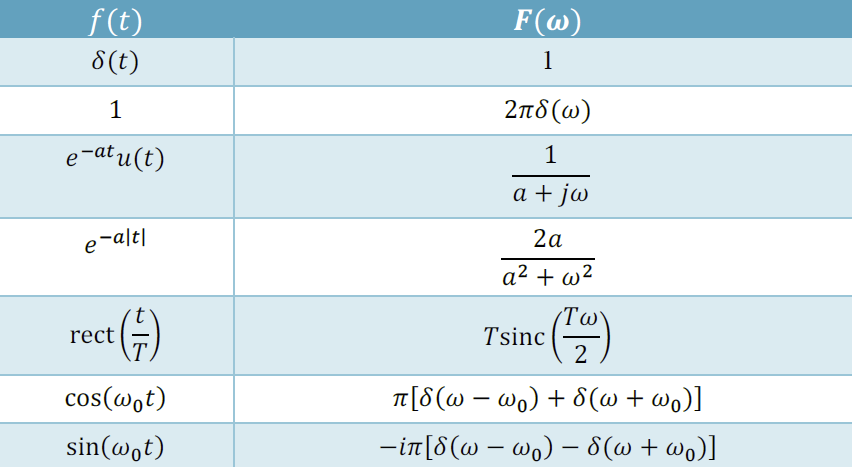
更多参见 key texts,比如 Continuous and discrete time signals and systems P204
找了个表格:链接 不过部分符号和我们学的不太一样,嗯……但是只要把 sinc 搞明白其他也差不多。如果找到了更合适的表格会在这里更新的。
week 5

第5周看上去东西是最多的,但实际上我贴上公式表格之后也没什么好写的了,毕竟我们计算也没有深入。
week 6
Sampling 采样
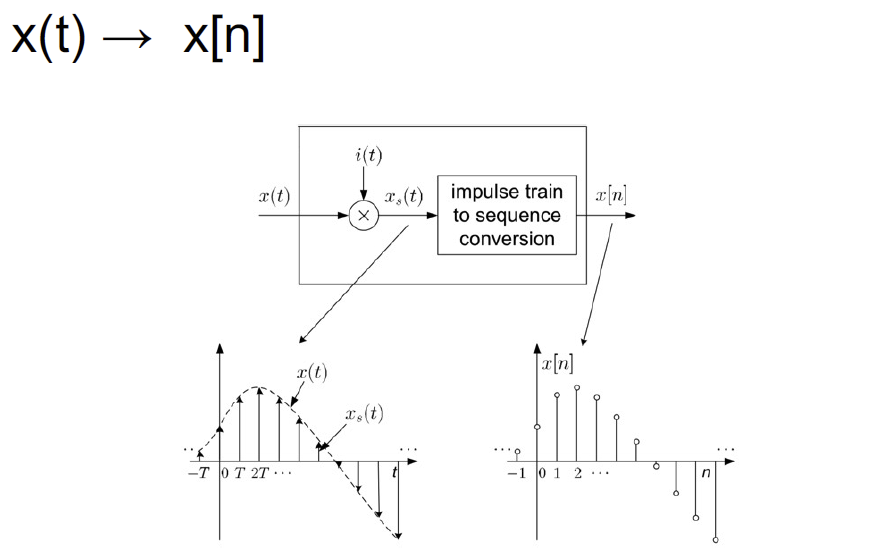
- 当\(x(t)\) 采样变为 \(x[n]\) , 若采样间隔为 T,则 \(x[n]=x(nT)\)
采样过后的离散函数从数学上来说就是一堆 \(\delta(t-nT)\) 叠加,和正常的函数的性质基本一致 :
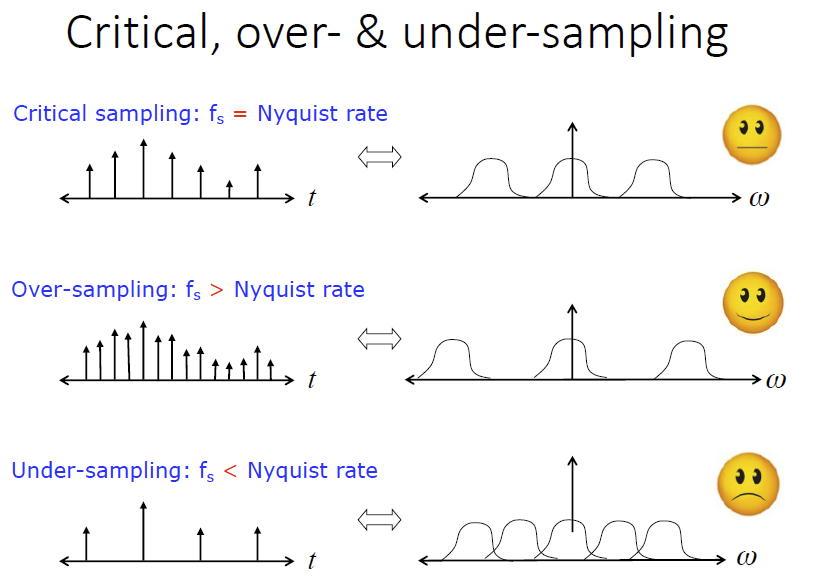
Nyquist-Shannon Sampling Theorem 奈奎斯特–香农采样定理

对于带宽有限的连续信号,其信息可以被足够密集的离散采样完全重现。
- 带宽有限 :时域信号转换到频域后,有其最高频率\(f_B\) (all of its frequency components lying in the band 0 ~ \(f_B\) Hz)
- 足够密集 : 采样频率大于 Nyquist
rate 奈奎斯特频率
- Nyquist rate :\(2f_B\)
- 完全重现 :采样后的信号和原信号在信息量上没有任何差别。
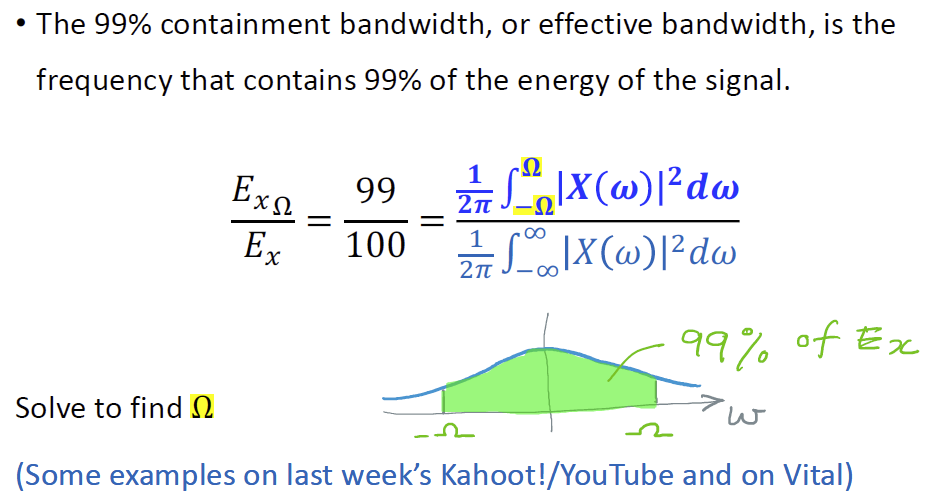
Effective Bandwidth 有效带宽
大部分模拟信号的带宽都是无穷大的,我们需要近似。
当该范围内的频域积分达到总积分的99%,即为有效带宽范围。
week6 其他较重要ppt :
3.2 history 由来
理科的结论与历史无关,但历史有助我们理解所学。
把某一函数分解成一系列正弦波,虽然看上去和信号这种东西天然契合,但实际上它最早是为了分析传热。
我们知道,对于传热这种物理问题,每一点上的温度由且仅由他周围的温度所决定,需要解偏微分方程。而对于热量在空间上呈正弦波分布的情景,其温度变化仅仅是正弦波的振幅逐渐变小而不会出现复杂的函数变化,是好的。
因此,当傅里叶发现所有周期函数都可以被分解成正弦波级数的时候,他意识到这种方法在传热学中大有可为,因为正弦波在传热里是那样好算,我们可以先把任意一种情形分解成这一类简单的函数之后再复原回去,许多计算就变得相当简单。
周期信号都可以表示为成谐波关系的正弦信号的加权和,非周期信号都可以表示为正弦信号的加权积分。
傅里叶也因此名垂不朽。
而在信号这一应用场景中,空间上分布不均的温度变成了随时间变化的信号取值,被赋予了传递信息的含义。(而且不用求解偏微分方程,可喜可贺,可喜可贺。)
现如今,由于傅立叶变换的良好性质,它已经发展成为一门叫做调和分析的学科。当然,这内容已经太过深入了。
3.3 domain 域
以信号分析的视角来看,Fourier Series / Fourier Transform 是一种变换,将时域信号转换到频域来分析。这种转换并没有改变我们原先的那个信号,他仅仅是用不同的视角去看同一个东西。比如我们可以通过仪器把声音转化成随时间变化的振幅曲线,我们看到的便是时域信号;但是同样的信号我们用耳朵听,我们分辨出的音色高低,就是不同频率的正弦信号及其叠加的效果,所以我们耳朵听到的是频域信号。
但实际上这只是两种视角而已。客观上来讲,我们感知到的都是同一个信号。
Fourier transform 把同一个信号在两个域中互相转换,方便我们计算。它是一种工具,一种分析,但不是一种会实打实对信号产生扭曲的操作。而我们学到的所有技巧都是教我们如何在两个域中相互转换,又如何将这两种不同的视角通过一些数学公式联系在一起,这样就可以随意转化视角来更方便地解决问题。
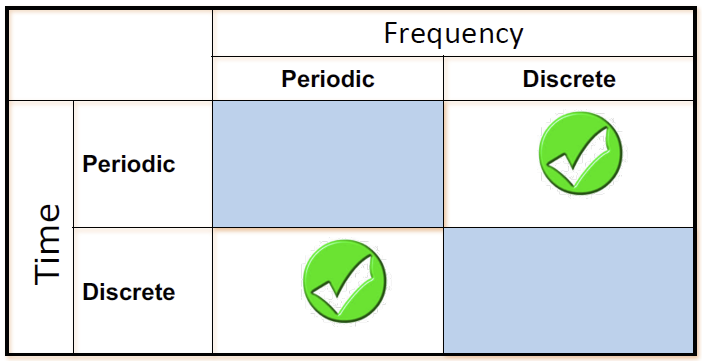
值得注意的是周期和离散这两个性质在Fourier Transform中的对称性:
| 时域 | 频域 |
|---|---|
| 周期 | 离散 |
| 离散 | 周期 |
Fourier Transform是一种积分变换。积分意味着变换会涉及到整个函数的全局性质,而周期和离散这两个东西它们都是整个函数的性质,而不是某一处的局部特性。不像求导,只需要知道这个函数在 这里 的导数是多少就好了。积分变换它一定是描述了函数整体性质的,牵一发而动全身,这是很重要的一点。
通过域本身的性质去看也很好理解,如果我在某个时域信号里加入某一频率的正弦分量,虽然在频域里只是某个\(\omega\)处变大了点,由于正弦波不随时间变化的性质,它会在时域里影响到整个函数;反之亦然。
不管是Fourier Series还是Transform,他们都是基于这两个域所进行的操作,讲完了域,接下来就可以讲讲Fourier了。
3.4 Fourier Transform 傅里叶变换
没写完,待更新( ゚∀。) 主要是感觉写出来的和老师上课讲的没有区别,可能还不如直接贴PPT。但傅里叶变换这样应用广泛且影响深远的概念肯定不止这样一种理解方式和教学思路,所以我目前在读书。进度参见 “《傅立叶分析导论》研读笔记 ”。