ELEC270 W2

ELEC270 WEEK2

前言

本博客草草创建，简陋不堪。本人才疏学浅，笔记也不过给诸君作一参考。如有疑惑/错漏/建议 还请使用这个匿名提问箱，我会一一回复。

https://www.tapechat.net/uu/5r0pL8/ZV9H0543

本周仍是基础，且只涉及出现过的数学概念所以只要前两年数学及格相信大家都懂。

2.1 Elementary Functions 基础方程的使用

这里要是不会参见week2PPT p9-22。

不过 \(\delta(t)\) 的sifting(sampling) property 采样特性 值得提一嘴：

对于 \(\int_{-\infty}^{\infty}{ x(t)\delta(t-\tau) dt}\) , 由于 \(\delta(t-\tau)\) 无限窄但积分为1，相当于在 \(t=\tau\) 处取了函数值。于是—— \[ \int_{-\infty}^{\infty}{ x(t)\delta(t-\tau) dt}=x(\tau) \]

效果是在 \(t=\tau\) 处对 \(x(t)\) 采了次样。

在数学上，如果我们想把某连续信号采样做成离散信号就可以通过多次使用这个式子来完成。

2.2 cross correlation 互相关

额，这玩意的中文名就叫互相关，不是我少打一个字……

说实话，这玩意要不是写笔记我都注意不到，当时觉得就是卷积前奏没有管他，但仔细一看发现这东西本身还是有意义的。

先上定义： \[ R_{xy}(\tau)=\int_{-\infty}^{\infty}{ x(t)y(t-\tau) dt} \] 啊啦啊啦，这不就是把其中一个函数平移了一个 \(\tau\) 的距离，然后再相乘积分一下吗？

是的，就是这么简单。但是这个操作有一个很重要的用处——判断两个信号的相似度。如果把 \(\tau\) 设为0，那么下周的傅立叶级数每一级的系数都是通过互相关算出来的。

以及这个操作不像卷积一样有良好的计算性质，比如说它不满足交换率 \(R_{xy}(\tau)\neq R_{yx}(\tau)\) ，用的时候稍微要谨慎一些。不过这东西也不像卷积一样有那么多复杂进阶操作啦

2.3 auto correlation 自相关

有了互相关，就有自相关。数学的想象力唯有在这方面能够如此……好吧，其他地方也挺跃进的。 \[ R_{xx}(\tau)=\int_{-\infty}^{\infty}{ x(t)x(t+\tau) dt} \] *注意，此处不是 \(t-\tau\) 而是 \(t+\tau\) 了！别问我为啥，我也不知道。不过由于自相关是自己和自己相关，函数结果是个偶函数，\(+\tau -\tau\) 其实结果都一样。

这两个相关操作还是蛮重要的，你想想，假设我们的信号上面有噪声，如果我们使用相关操作会产生什么情况？噪声是随机的，没有规律，也就没有相关性。所以噪声相关后就会相互大大抵消，原函数就被凸显出来了~

2.4 convolution 卷积

相信大家对convolution这个词语都不陌生，因为相关的概念和计算我们早在大二上学期MTH101上就已经学过。(好吧，三巨头也是学过的……其实我们拉普拉斯变换都学过了）

不过这东西概念虽然简单，但他是个很基础的操作。这意味着它可以和一些很复杂的概念打一套组合拳，MTH101就有过一些涉及卷积的题目但是七弯八绕让人摸不着头脑。

如果你直接上中文网站去搜关于卷积的定义，他可能会告诉你要把其中一个信号反褶过来然后再平移过去相乘得到一个最终的结果。你如果耐心的看完这些解释，其实也看得懂，而且也很符合卷积这个词。但对于信号分析来讲，这些操作就显得有些意义不明，非常奇怪。在这里我尝试这一操作的物理意义讲明白。

首先来看卷积的定义式： \[ x(t)*y(t)=\int_{-\infty}^{\infty}{ x(\tau)y(t-\tau) d\tau} \] 我们看到，其中有一个函数的自变量\(\tau\)反过来了。为什么会反过来呢？

我们考虑一个气球摊位，小朋友们排队买气球。由于气球质量不佳，会漏气，随着时间变得越来越小。我们可以使用一个函数描述这个过程，气球体积函数：\(V(t)\) 。小朋友买到了气球之后，气球失去了摊贩的持续供气变得越来越小，其体积\(=V(t)\)

那么现在有一堆小朋友排队买气球。假设我们取其中某个时间点进行观察会发现，越早买气球的小朋友气球越小，对应\(V(t)\)里更大的 t ；越迟买气球的小朋友气球越大，对应\(V(t)\)里更小的 t 。

如果把买气球也看作一个函数\(=M(t)\), 有下总结：

\(M(t)\)中 t 越大，对应 \(V(t)\) 中 t 越小；

\(M(t)\)中 t 越小，对应 \(V(t)\) 中 t 越大；

你看，在这个例子里虽然原本这两个函数都和时间相关，使用时间变量t。可一旦在情景中进行分析，二者之间的 t 却呈相反的关系。

而这也就是卷积中为什么有一个函数的\(\tau\)会变成\(-\tau\)的原因。卷积是两个信号之间的相互作用，而相互作用意味着我们有一个开始作用的时间和一个作用的总时间。

开始越早，总时间就越大；

开始越迟，总时间就越小。

接着为了让二者可以被统一表达，我们需要将其中某个的时间轴反过来，对应于传统解释的反褶。因为相反是相对的，所以谁反过来都一样，所以卷积满足交换律：\(x(t)*y(t)=y(t)*x(t)\)

考虑到刚刚那套分析我们只是取了其中某一个时间点 t ，那么对于所有的时间点我们都可以进行这样的分析，这也就是定义式里 t 的作用——对每一个时间节点的分析。这也就对应于传统讲解里的平移，最终会让卷积生成一个新的函数。对于不同的应用场景，卷积生成的结果会有不同的含义。

信号与信号之间的相互作用，这一听就知道是信号分析里最主要的研究对象。在接下来的各种题目乃至授课中我们都会频繁遇到卷积操作，所以大家一定要对于这个东西了如指掌。

重要性质： \[ x(t)*\delta(t-\tau)=x(t-\tau) \]

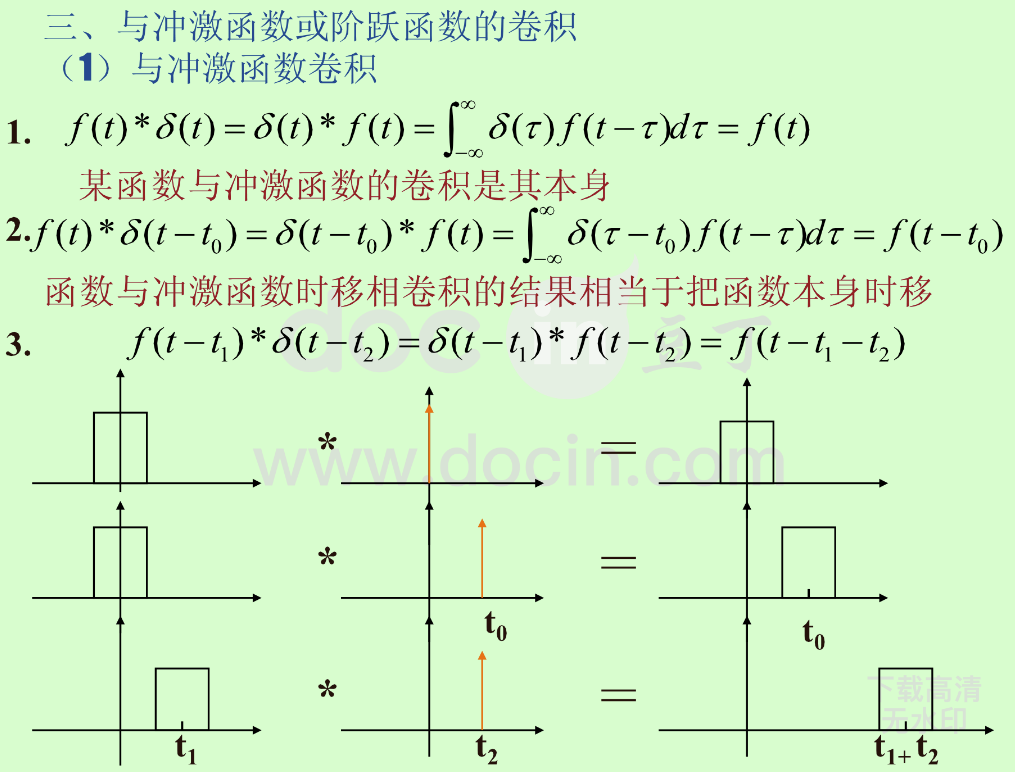
当然卷积也不仅仅是在信号分析里面会用到，比如说在CV里这玩意也是一个非常基础的操作了.不过那还涉及矩阵什么的而且这里是信号与系统笔记就先不暂且展开了，之后如果有时间的话再说吧(=ﾟωﾟ)=

要是有啥笔记以外的问题想要探讨，其实咱们270已经有一个微信群了。但你要是不嫌弃来加一下校友力给的群呢……那可太好了，毕竟我在恰烂钱嘛~ 这里人少，咱们有问题就可以问( ﾟ∀。)（尝试找到该群存在的意义