ELEC270 W1

发表于 2021-10-24 更新于 2022-01-21 分类于 ELEC270 阅读次数： Valine：

初来乍到，姗姗来迟

ELEC270 WEEK1

开局做实验写report再加上一个数据库，还没反应过来的我被一套连招打得猝不及防･ﾟ( ﾉд`ﾟ)，再加上这学期我想摆脱愚笨的PDF-公众号体系，还要从零开始摸索搞个博客（也就是你现在看到的这个网站）……于是笔记一拖再拖，以至于week5都要到来了，我才匆匆把week1的笔记本补上。

不过这几天应该会快速跟上教学进度。

笔记原是兴趣与复习所求，不过后来机构指校友力找上门来，我喜上眉梢恰了这份烂钱（?），这便成了一份工作。听上去属于是恶堕了，但其实对我而言没什么差别。相反，我只能对它更加负责了。（还有一个机构搞的微信群，为了保证阅读复习时的纯洁性我就放在末尾了——）

本博客草草创建，简陋不堪。本人才疏学浅，笔记也不过给诸君作一参考。如有疑惑/错漏/建议还请使用这个匿名提问箱，我会一一回复。

https://www.tapechat.net/uu/5r0pL8/ZV9H0543

2825a24c118865733fed378243464f4a

咱们这课，说是ELEC，其实就是打了MTH开头的课。但我要这么说，数学系的同学估计血压那是轰的一下就滋上来了，毕竟咱们这里不少东西还是工程味儿浓厚。只能说，啊，工程数学，工程数学。

信号与系统，顾名思义，这是研究信号，研究发送与接受的科目。所以当我们在学这门科目的时候，思考方式要足够灵活，很多乍一眼有点迷惑的东西，其实是因为现实中的交流有其对应之存在。

1.以值域划分

2.以定义域划分

3.以周期划分

周期信号 Periodic Signal ——————定时重复的信号（有周期 T）
非周期信号 Non-Periodic Signal ———无法完全重复的信号（周期 T 无穷大）
- 为什么非周期信号要说的那么拗口？因为部分重复是可能存在的，别被迷惑了。

4.以解析性划分

5.以对称性划分

6.以物理性质划分

功率信号 Power Signal ———————— 总能量无限平均功率有限（如交流电源）
- 计算周期信号功率应使用公式 \(\frac 1 T \int^{T}_{0}{ f(t)^2 dt}\)
能量信号 Energy Signal ———————— 总能量有限平均功率为0 （如电池）
- 计算总能量应使用公式 \(\int{ f(t)^2 dt}\)
- 哪怕对于公式变为求和的离散信号也是如此，把每个离散值都当做宽度为1的长条形就好。
- 直接积分和能量计算不仅结果不同，还可能改变有/无限的性质（参考\(\frac{1}{x}\)和\(\frac{1}{x^2}\)积分结果的异同）

上面所有划分方法都是相互平行互不干扰的，不存在在某个划分下是某种类那么在另一个划分下就必然是某种类的说法。

（除了随机信号。一般来说随机信号不会是能量信号，而是功率信号。不过这个结论我也没有问过老师，等什么时候问到了结果会在此更新。）

\(u(t)\) Unit step

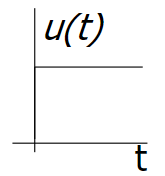\[ u(t)=\left\{ \begin{array}{rcl} 1 & \mbox{for} & t\geq0 \\ 0 & \mbox{for} & t<0 \end{array}\right. \]
\(r(t)\) Unit ramp

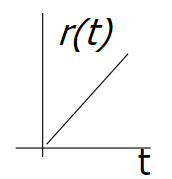\[ r(t)=\left\{ \begin{array}{rcl} t & \mbox{for} & t\geq0 \\ 0 & \mbox{for} & t<0 \end{array}\right. \]
\(\delta(t)\) Unit impulse

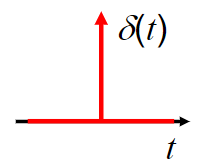\[ r(t)=\left\{ \begin{array}{rcl} \infty & \mbox{for} & t=0 \\ 0 & \mbox{for} & otherwise \end{array}\right. \] \(\delta(t)\) 的定义有点奇特，需要单独说一下。